Suppose that we have the equation $ax^2+by^2+cz^2=0, a,b,c \in \mathbb{Q}$.
Without loss of generality, we suppose that $gcd(a,b,c)=1$.
Also, we can consider that $a,b,c$ are square-free.
We can suppose that $(a,b)=(b,c)=(a,c)=1$.
Proof of the last sentence:
Let $d=(a,b)>1$
Since $a,b$ are square-free $\Rightarrow d$ is also square-free. $$a=da' \\ b=db'$$ $$\Rightarrow (a',b')=1$$
It stands that $(d,c)=1$.
Proof:
Let $d'=(d,c)>1$
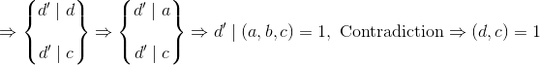
So, when $(x,y,z)$ an integer solution of $ax^2+by^2+cz^2=0 \\ \Rightarrow d(a'x^2+b'y^2)+cz^2=0 \\ \Rightarrow d \mid cz^2, (d,c)=1 \Rightarrow d \mid z^2$
Since $d$ is square-free, $d \mid z^2 \Rightarrow d \mid z \Rightarrow z=dz'$
The initial equation: $$a'x^2+b'y^2+(cd)z^2=0$$
We concluded to an equivalent equation, where $(a',b')=1$
With the same procedure, we prove that $(a,b)=(b,c)=(c,d)=1$
Could you explain me why, having the equivalent equation, we conclude that $(a,b)=1$ ?