I’m going to discuss the action of Spin(3) on Euclidean vectors. This thing has several alternative names: “versors”/“rotation quaternions”, “quaternionic adjoint representation”, “quaternion action on vectors”, “weight-1 irrep of SU(2)”, but I did not encounter visualization concepts that are illustrative and correct simultaneously.
My best effort to show both the group operation (as composition of great-circle arcs) and its action (also on the unit sphere) resulted in
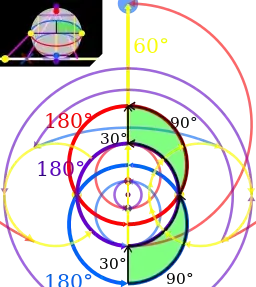(rendered from File:Spin_180,60.svg).
This concept can be technically improved (made into animation or even an interactive applet), but tracing 3D rotations in the form of motions on a sphere requires some familiarity with spherical geometry. Does anybody know a better concept that can explain Spin(3), presumedly using a common 3D geometrical intuition? It is expected really to show Spin(3) elements in some way and how to multiply them, not only substantiate the π1(SO(3)) thing.
