Associates in the ring of continuous real-valued functions on $[0,1]$

Question

I have tried to give a proof of the following theorem but I feel very unsure and would be very grateful if someone would check it for me

Many thanks!

Theorem. Let $R$ be the ring $C[0,1]$ of continuous real-valued functions on the interval $[0, 1]$ (with pointwise operations). If $f, g \in R\setminus\{0\}$ satisfy $f \,|\, g$ and $g \,|\, f$, then there is some unit $u \in R$ such that $f = ug$.

Proof. First observe that the units in $C[0,1]$ are precisely the functions which are nowhere zero.

Since $g\,|\,f$ (say $f=sg$) and $f\,|\,g$ (say $g=tf$) we have

1) $f(x)=0 \Leftrightarrow g(x)=0$;

2) $s(x)=0 \Rightarrow f(x)=0$;

3) $t(x)=0 \Rightarrow g(x)=0$;

Thus we reduce to the case where $f$ and $g$ are both non-units.

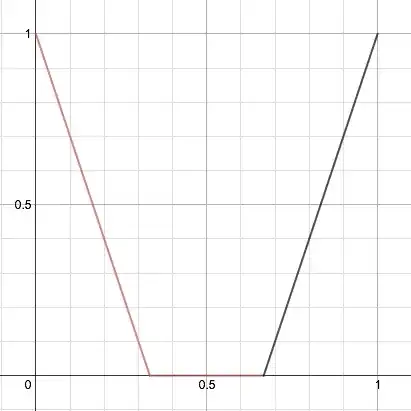
There is some $(a,b)\subseteq[0,1]$ such that

1) $f$ and $g$ are both non-zero on $(a,b)$;

2) either $f(a)=g(a)=0$ or $f(b)=g(b)=0$ (wlog we assume the former).

We see that $s(x)=\dfrac{1}{t(x)}$ for all $x \in (a,b)$ and so, since $t$ is bounded, we cannot have $s(a)=0$.

It follows that $s$ is a unit. Q.E.D.

Answer 1

Consider this piecewise linear function as $f(x)$:

Now let $u(x)$ be the following piecewise linear function:

Let's look at your proof with $f(x)=g(x)$. We can use the functions $s(x)=u(x)$ and $t(x)=1$ because $f(x)=u(x)f(x)$ and $f(x)=1*f(x)$.

The problem is that you can't just use any $s(x)$ and $t(x)$, you need to construct them. [Since you are only asking for a check of the proof, I won't propose a solution.]

Answer 2

This is not true as it is shown by a simple example of Kaplansky which can be found in this answer.