I've two spheres in cartesian space: $(x_1, y_1, z_1, r_1)$ and $(x_2, y_2, z_2, r_2)$.
They don't intersect each other.
I want to calculate the conical frustum tangent to these two spheres.
In particular, I need to find the center point and the radius of bases of conical frustum.
How can I do it?
EDIT:
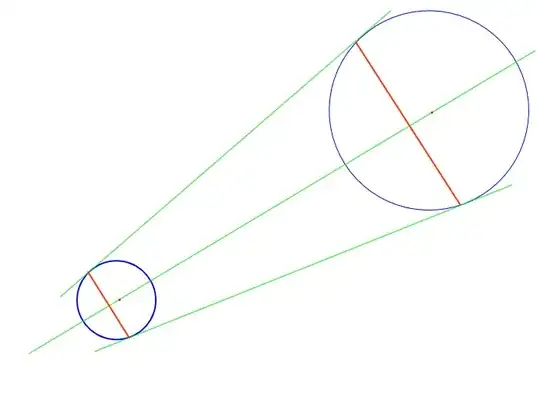
My problem is represented in this image (che 2D equivalent one).
I need to find red segments, that in the 3D space problem are circles. In order to find these I need to know (always in 3D) the center and the radius of red shapes, that always in 3D are conical frustum bases.