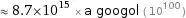I know that today it is almost impossible to find someones Seed. But what happens in the future. Will it ever be possible that a very fast supercomputer is checking million seeds per second to find Seeds with a balance. Maybe someday it will be like bitcoinmining for the people. They let many supercomputer run and if one of them finds a balance it will send the funds directly to the address of the miner...
2 Answers
The probability of finding a special seed is 27^81 = 8.71 * 10^115.
If we assume that there are 1 trillion seeds, the probability of finding a seed with a balance is 8.71 * 10^103 .
If we assume now a Computer can scan 1 Billion Seeds per second, it would take him 2.7647654 * 10^87 Years, to find one seed with a balance.
This is a pretty long time, I think we are save.
- 84
- 1
First, Iota seeds consists of 81-trytes (243-trits) with have three levels of safety [ 1]:
A security level determines the number of rounds for hashing, which means that a single seed can have 3 different accounts.
81-trits (low security)
162-trits (medium security)
243-trits (high security)Technically speaking, a single seed has 3 accounts. The same key index on a different security level returns a completely different address. Make sure you keep track of your security levels similarly to your key indexes, as it will be needed for spending your inputs [ 6].
A seed of 81 trytes results in :
87189642485960958202911070585860771696964072404731750085525219437990967093723439943475549906831683116791055225665627 possible probabilities
Very important:
To "hack" an address one needs to try random seeds, a single attempt can succeed with
1/(27^81)probability because it depends on the number of the addresses, not on the number of the seeds [ 3]
By the fact that IOTA using Winternitz's unique signatures (post-quantum signature) [ 1] [ 4] [ 5] You can not use the Shor Algorithm to reduce complexity or attempts, as you can with a Bitcoin address that uses Elliptic Curve Cryptography, for example.
It is a consensus among cryptologists that any value above 2^80 is computationally infeasible. So, by answering your question, the chance of a supercomputer finding a seed is pretty remote. Since a quantum computer does not take advantage of an ordinary computer, in this case
As for security levels, I'm not sure. But, as far as I know, they generate one more delay in the attempts since they are levels of hash rounds. And this (I'm not sure of the following statement) increases hashspace for ^security level (This is not the amount of possible seeds) and *security level by attempts
e.g. (Hashspace increment)
- 81 trits =>
27^81 ^1 (low security) - 162 trits =>
27^81 ^2 (medium security) - 243 trits =>
27^81 ^3 (high security)[Citation needed]
e.g. (Attempts increment)
- 81 trits =>
1* 27^81 attempts (low security) - 162 trits =>
2* 27^81 attempts (medium security)//Two times more attempts - 243 trits =>
3* 27^81 attempts (high security)[Citation needed]
References:
[1 ] https://iota.readme.io/v1.2.0/docs/seeds-private-keys-and-accounts
[2 ] https://www.wolframalpha.com/input/?i=27%5E81
[3 ] Why aren't seeds longer than 81 trytes more secure?
[4 ] https://eprint.iacr.org/2011/191.pdf
[5 ] https://www.e-reading.club/bookreader.php/135832/Post_Quantum_Cryptography.pdf#page=45
[6 ] http://learn.iota.org/tutorial/generating-addresses-learn-the-basics
- 435
- 3
- 8
-
For those who voted negative. Could you give me more information so that I can improve my answer? – Avelino Dec 10 '17 at 15:58