FSK or M-PSK for weak signal communications?

Question

Popular amateur radio "below-the-noise-floor" communication modes (such as JT65, et.al.) seem to mostly use FSK, whereas NASA's deep space network appears to use M-PSK for (extremely) weak signal telemetry. Why would one choose one modulation scheme over the other when designing a (new *) protocol for extremely weak signal QSOs?

(assuming the next layer uses typical interleaving/FEC/ECC/convolutional coding for multi-bit and burst error tolerance, etc.)

(* as full specs do not appear to be available for many of these existing amateur radio modes)

Answer 1

We'll have to lay down some rules for the comparison:

• For a fair comparison, the energy per bit in each scheme under consideration is constant. So, a "fair" alternative would be switching from 4-PSK to 8-PSK while maintaining the same transmitter power and halving the symbol rate.
• Likewise, the noise spectral density is constant.
• Forward error correction, interleaving, etc. are not considered, as it's assumed these methods would be applied with equal efficacy regardless of the underlying modulation.
• "Weak signal" means we wish to maximize the probability of correctly decoding a bit under noise-limited conditions.
• The comparison is in an additive white Gaussian noise (AWGN) channel, that is one where there's only white noise, and no multipath, etc.
• Frequency shift keying and phase shift keying are the only options.
• Implementation details (complexity, non-ideal properties of the receiver, etc) are irrelevant.

If we consider just binary phase shift keying or frequency shift keying, PSK wins handily. You can even halve the symbol rate and use 4-PSK, and get the same performance as 2-PSK in half the bandwidth. The bit error rates for binary PSK and coherently detected¹ binary FSK are:

$$ P_{b(BPSK)} = Q \left( \sqrt{2E_b \over N_0} \right) \tag 1 $$

$$ P_{b(BFSK)} = Q \left( \sqrt{E_b \over N_0} \right) \tag 2 $$

Where $N_0$ is the noise spectral density, $E_b$ the energy per bit, and Q a scaled version of the error function:

$$ Q(x)=\operatorname {erfc} \left({\frac {x}{\sqrt {2}}}\right),\ x\geq 0 $$

Note the $2$ in the $2E_b$ factor of equation 1 means transmitter power goes twice as far for BPSK.

4-PSK has the same BER as 2-PSK: it is effectively 2 orthogonal 2-PSK signals. It's easy enough to understand intuitively, examining the constellation diagram:

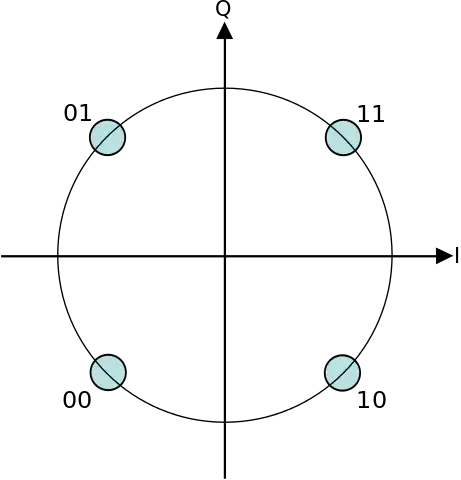
Each symbol contains two bits. If we're left of the vertical axis, the first bit is a 0. Otherwise it's a 1. Since the first bit is determined only by the position left or right, the position up or down is irrelevant, or orthogonal.

Orthogonality is key. Taking this idea further to 8-PSK results in an increase in BER since the symbols are no longer orthogonal.²

By Splash - Own work, CC BY-SA 3.0, Link

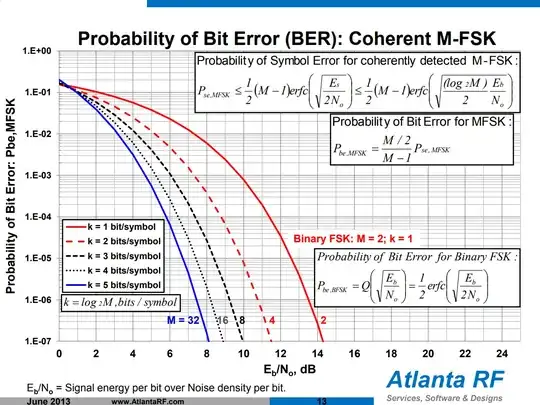
Now back to FSK. With binary FSK there are two tones, each conveying a 1 or a 0. But as with PSK the order can be increased: if we have 4 tones, each maps to two bits. With eight possible tones, a single tone conveys 3 bits.

With PSK, as the order was increased the bandwidth went down and the error rate went up. With FSK the opposite happens. This is because unlike PSK, with FSK we can add more tones while retaining orthogonality, provided there's sufficient bandwidth to space them apart.

Why does this work? Imagine a receiver that looks at a single frequency and has to decide if a tone is present there or not. At some transmitter power and tone period this will work reliability, and each period communicates one bit. Say tone present = 1, and absent = 0.

Now if there are 16 such receivers, the detection of a tone present communicates not one bit but four (there are sixteen possible combinations of four bits). The more possible tones, the more bits are communicated per tone, with no additional transmitter power.

Or equivalently, we could slow the symbol rate but hold the bit rate constant, putting more time and thus energy into each tone and making it easier to detect. Conveniently, decreasing the symbol rate also decreases the minimum spacing between the tones to maintain orthogonality.

Atlanta RF provides a nice graph:

The weak-signal performance-enhancing properties of wide bandwidths are reflected in the (modified here to assume white Gaussian noise) Shannon-Hartley theorem:

$$ C = B \log_2 \left( 1+\frac{S}{N_0 B} \right) $$

Where:

• $C$ is the channel capacity, in bits per second
• $B$ is the bandwidth, in hertz
• $S$ is the signal power, in watts
• $N_0$ is the noise power spectral density, in watts per hertz

So while increasing the bandwidth does decrease the SNR term, it increases the $B$ term faster.

---

1: Coherent FSK detection is the most complex, and most accurate method of detection.

2: However, it does improve spectral efficiency. Many applications are bandwidth limited, so higher-order constellations are popular. For example, Wi-Fi uses at the higher data rates 64-QAM to cram the highest bit rate possible in the limited bandwidth available.

Answer 2

First, we should be clear that neither of these modulation methods allow signals below the noise floor to be decoded. The oft quoted -dB figures for FT-8 et al are really quoting the signal strength below the noise floor of an audio bandwidth of ~ 2.5 kHz. But through digital signal processing of the audio channel, these modes are actually using an occupied bandwidth of 50 Hz or less. So if the reported SNR ratio was based on the actual data bandwidth, the reported signal strength would be well above the noise floor. The noise floor in dB (watts) of a receiver is determined by the bandwidth of the receiver:

$${Noise Floor} = 10\log_{10}(kTB) \tag 1$$

where k is the Botlzmann's constant (1.38064852×10⁻²³ J/K), T is the temperature in Kelvins, and B is the bandwidth in Hertz.

So using equation 1, we can see that a 50 Hz receiver bandwidth has ~17 dB noise floor advantage over a 2.5 kHz receiver bandwidth. Since the noise floor of a 50 Hz bandwidth is ~17 dB lower, the signal to noise ratio (SNR) expressed in dB improves by the same ~17 dB. This is the same effect we see when comparing the ability to copy an SSB signal compared to a CW signal using a narrower receive bandwidth. But reducing the bandwidth comes at the price of a reduced data rate reaching the limit expressed by the Shannon-Hartley formula:

$$C=B\log_2(1+\frac{S}{N}) \tag 2$$

where C is the maximum channel capacity, B is the channel bandwidth in Hertz, S is the signal strength in Watts, and N is the noise power in Watts.

Regarding the modulation modes, PSK has an approximately 3 dB SNR advantage over other modes. The reason we do not see it commonly deployed on HF is that the standard amateur radio transceiver does not support carrier phase modulation so AFSK or APSK are the only viable means of modulation. If we were to develop special purpose HF transceiver capable of supporting carrier PSK modulation, we could capture an additional 3 dB of SNR.

MPSK reduces the complexity of the receiver since there is no requirement to acquire/track the carrier as there would be with PSK. Here is a synopsis of a decoding technique described in IEEE Transactions on Communications (ISSN 0090-6778); 38; 300-308:

A differential detection technique for MPSK (multiple-phase shift keying), which uses a multiple-symbol observation interval, is presented, and its performance is analyzed and simulated. The technique makes use of maximum-likelihood sequence estimation of the transmitted phases rather than symbol-by-symbol detection as in conventional differential detection. Thus, the performance of this multiple-symbol detection scheme fills the gap between conventional (two-symbol observation) differentially coherent detection of MPSK and ideal coherent of MPSK with differential encoding. The amount of improvement gained over conventional differential detection depends on the number of phases M and the number of additional symbol intervals added to the observation. What is particularly interesting is that substantial performance improvement can be obtained for only one or two additional symbol intervals of observation. The analysis and simulation results presented are for uncoded MPSK.