How does an SWR meter really work?

Question

For ham radio operators, the SWR meter is a ubiquitous piece of equipment. There are dozens of standalone models on the market and most modern transceivers and antenna tuners have this functionality built in.

Any ham with an interest in antennas has probably had their hands on SWR meter. Operating them is relatively straight forward but understanding how they work seems to be another matter.

There is an abundance of descriptions in texts, magazines, and on the Internet that attempt to describe how an SWR meter (or its close cousin a directional watt-meter) works. Some of these even state that the meter is able to actually separate the forward and reverse power, voltage, or current. After looking at the schematics for many of these devices, this seems dubious. Others attempts at describing its underlying mechanisms, such as How Should this SWR Meter's Directional Coupler Work don't seem to come to a consensus.

How do these instruments really work? What is the basic math behind it?

Answer 1

Dispelling the Myth

To begin with, the typical HF SWR meter does not have the ability to separately sample the forward and reverse power, voltage, or current. Any description of the device or its circuitry that suggests this capability is flawed. We can show this empirically with two different experiments.

Experiment 1

Connect a 100 ohm resistor directly to the output of a 50 ohm SWR meter (no coax cable) and directly connect the input of the SWR meter to the transmitter (no coax cable). The resistor will dissipate all the power that the transmitter can put out into the 100 ohm load - no reflections of voltage, current or power since there is no transmission line. Yet the meter will show a 2:1 SWR.

Experiment 2

Connect the transmitter directly to the input of the 50 ohm SWR meter. On the output of the SWR meter connect a 75 ohm coaxial cable and attach a 75 ohm load to its end. Since the load matches the Z_o (characteristic impedance) of the coax cable, there are no reflections of voltage, current or power on the coax cable. Yet the meter will show an SWR of 1.5:1.

How Does it Work?

The typical HF SWR meter works by sampling the complex voltage and current at the point of insertion from which it calculates the effective SWR at the point of insertion on a transmission line with a characteristic impedance of 50 ohms (or whatever impedance for which the SWR meter is designed).

The term "effective" is used here because the calculation is performed regardless of whether a transmission line is present or not and regardless of the actual characteristic impedance of any transmission line that is present.

Sampling the Voltage

SWR meters use one of three different methods to sample the complex voltage at the point of insertion.

^{simulate this circuit – Schematic created using CircuitLab}

In each case, the voltage sampling circuit steps down the higher voltage that is present on the transmission line at the point of insertion to a more manageable lower voltage for the SWR meter circuit. In the case of the resistive and capacitive divider circuits, the upper element is typically adjustable to allow the SWR meter to be calibrated (more about this later).

The voltage present on the transmission line at the point of sampling is the complex sum of all of the forward voltages plus the sum of any reflected voltages resulting from a mismatched load and source. This can be expressed as:

$$V_\text{line}=V_f+V_r \tag 1$$

where V_f is the complex forward voltage and V_r is the complex reflected voltage at the point of sampling.

The sampled voltage from any of the above circuits can then be expressed as:

$$V_1=(V_f+V_r)*k_1 \tag 2$$

where k₁ is the scaling constant as determined by the voltage sampling circuit design.

Sampling the Current

Nearly every SWR meter uses the same technique to sample the complex current that is present on the transmission line at the point of insertion. The technique involves a circuit that at first glance looks like a step-up voltage transformer with a load resistor on the secondary, but it is actually a special configuration known as a wide band current transformer.

A wide band current transformer converts the RF current that is passing through its primary side, to a proportional RF voltage on the secondary side. The conversion takes place by placing a load resistor (sometimes called the burden) on the secondary side. The load resistor must be much smaller than the characteristic impedance of the secondary side of the transformer for this current to voltage conversion to be proportional.

^{simulate this circuit}

The transformer is typically a toroid device with the center conductor of the transmission line passing through the hole of the toroid to form a 1 turn primary winding with the secondary winding wrapped multiple times through the toroid form.

The complex current that is present on the transmission line at the point of sampling is the difference between the forward current and the reflected current:

$$I_\text{line}=I_f-I_r \tag 3$$

where I_f is the complex forward current and I_r is the complex reflected current.

The complex voltage resulting from the sampled current using a wide band current transformer can then be expressed as:

$$V_2=(I_f-I_r)*k_2 \tag 4$$

where k₂ is the transformation factor, in volts/amp, as determined by the wide band current transformer circuit design.

Calculating SWR and Power

We now need a way to use the sampled voltage and current to calculate the SWR as well as the forward and reflected power. Most equations for calculating these values involve knowing the forward voltage and the reflected voltage. But so far we only have V₁ which is proportional to the sum of these complex voltages as shown in equation 2. There is, however, another way of expressing the complex current that is present at the sampling point that can help us:

$$I_\text{line}=\frac{V_f-V_r}{Z_o} \tag 5$$

where Z_o is the characteristic impedance of the transmission line, typically 50 ohms in amateur radio applications.

We can then substitute equation 5 into equation 4:

$$V_2=(V_f-V_r)*\frac{k_2}{Z_o} \tag 6$$

Now we subtract V₂ in equation 6 from V₁ in equation 2:

$$V_1-V_2=\Bigl((V_f+V_r)*k_1\Bigr)-\Bigl((V_f-V_r)*\frac{k_2}{Z_o}\Bigr) \tag 7$$

With a Z_o of 50 ohms, if we set the k₂ to k₁ ratio to 50, equation 7 is greatly simplified:

_{[Edit: Formulas 8 and 9 have been updated]}

$$V_1-V_2=((V_f+V_r)-(V_f-V_r))*k_1=V_r*2*k_1 \tag 8$$

Keeping the same k₂ to k₁ ratio but adding V₁ and V₂:

$$V_1+V_2=((V_f+V_r)+(V_f-V_r))*k_1=V_f*2*k_1 \tag 9$$

Since the 2*k₁ term is a constant known to the designer, it is easily factored out in subsequent applications of equations 8 and 9.

This adding and subtracting of V₁ and V₂ had in the past been accomplished with a switch on the SWR meter. Now it is more common that V₁ is fed into a center tap of the secondary of the wide band current transformer. With the appropriate circuit values, one leg of the transformer is then V₁+V₂ while the other leg is V₁-V₂.

Since power is proportional to voltage squared, equation 8 gives us a voltage that is proportional to reflected power while equation 9 gives us a voltage that is proportional to forward power. Each of these voltages are fed to their respective meter movement where the logarithmic scale drawn on the meter face does the conversion of the linear meter deflection, that is based on voltage, to power.

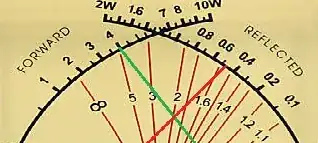
The conversion of forward power and reflected power to SWR is given as:

$$SWR=\frac{1+\sqrt{\frac{P_r}{P_f}}}{1-\sqrt{\frac{P_r}{P_f}}} \tag {10}$$

Or alternatively the conversion of V_f and V_r to SWR is given as:

$$SWR=\frac{1+(V_r/V_f)}{1-(V_r/V_f)} \tag {11}$$

The meter face pictured above shows the intersection of the two needles on the 2:1 SWR line which corresponds to equation 10 for the powers shown. The SWR meter designer simply plots a number of SWR values on the meter corresponding to the intersection of the forward and reflected powers.

Calibrating the SWR Meter

The typical calibration routine for the SWR meter is to attach a resistive load that is equal to the Z_o of the feedline directly to the output of the meter. A transmitter outputs the appropriate amount of power to the input of the SWR meter. The voltage dividing network is then adjusted such that P_r is equal to 0.

Since P_r is proportional to (V_r)², we can see from equation 7 that this adjustment is simply ensuring that k₂/k₁=50 for an SWR meter that has been designed for 50 ohm feedline.