1

At University I studied some stuff about modulation (only two lessons, so my knowledge is very limited) and as far I've understood, the FM signal is most reliable in audio than a AM signal, and it is more power efficient than AM modulated signal.

I would like to know which is the most efficient digital mode in FM for text and data transmission. Most efficient in term of bitrate and so data transmitted with minor errors, in order to use all the NFM channel bandwith

I suppose that AFSK is the only ""sub-modulation"" (is afsk a sub modulation of a fm signal ?) that I can use in FM signal, in particular with cheap fm handheld radio.

Gigi
  • 11
  • 2
  • 1
    "I would like to know which is the most efficient digital mode in FM" What does "efficient" mean to you? Energy efficiency doesn't matter for FM-modulated audio (the over-the-air-power is constant), so that's not it. Generally, the question "what is the best?" never has a single answer, you'll really need to define the conditions under which something has to perform and the metrics with which you measure its "goodness". There's a lot of reasonably good in-FM modulations (doing in-FM modulation is mathematically bad, but you might not have another choice, so, hm),but none of them is optimal – Marcus Müller Nov 20 '21 at 13:55
  • 1
    And we can mathematically prove that none of them is optimal for some kinds of channels. Generally, using the AM mode on your handheld and using that to do low-IF or baseband modulation is probably better in terms of spectral efficiency, so you might completely be off to a wrong start. Could you really edit your question and tell us exactly what you want to achieve, maybe taking care not to mix your requirements and your own suggestions? – Marcus Müller Nov 20 '21 at 13:58
  • The most efficient / best mode in any circumstance is the magical one that hasn't been invented yet. Without choosing parameters (like bandwidth vs. power or something), efficient has no meaning, and "most efficient" without scoping limiting conditions has even less meaning. – user10489 Nov 21 '21 at 06:30
  • I've modified my question in order to explain what I was meaning when I say "efficient". So, in term of quantity of data transmitted/errors – Gigi Nov 22 '21 at 09:35
  • 1
    Note also, in the US, symbol rate for wavelengths above 33cm are legally limited, so you can't have a symbol rate higher than that. Note that generally symbol rate == baud rate, but baud rate != bit rate. So by that definition, the most efficient mode for wavelengths larger than 33cm is the one that can pack the most bits per symbol while still staying in the audio channel bandwidth and not exceeding the legal symbol rate. – user10489 Nov 23 '21 at 05:29
  • So if I understand you correctly, you're looking for the "best" digital mode that works with narrowband FM radios with a channel width of 12.5 kHz. – rclocher3 Nov 23 '21 at 15:28
  • 1
    "Good, fast, or cheap; choose any two." –  Feb 24 '22 at 00:58

1 Answers1

1

I don't think the question can be answered as posed.

The spectral efficiency of a given channel, in bits per second per Hz (bps/Hz), will depend on the signal-to-noise ratio (SNR) in the channel as well as the minimum (bit) error rate that can be tolerated.

The figure below from this paper illustrates how these three three parameters relate for various modulation schemes for one particular bit error rate (BER) - in this case $10^{-2}$ (which is really poor). Presumably the family of curves would look different - perhaps much different - for higher BER's.

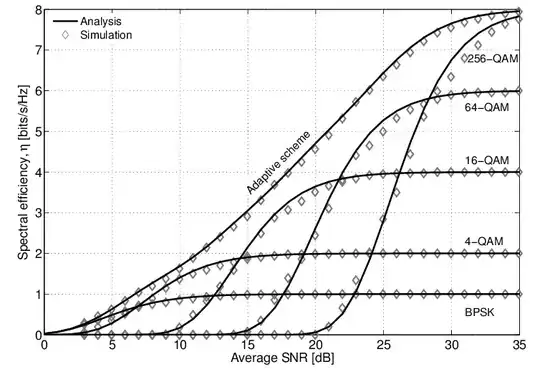
enter image description here

  • If the SNR is quite high - say better than 30 dB - then something like 7 bps/Hz or better could be achieved with 256-QAM (we'll come back to the "adaptive scheme" presented in the paper).
  • Notice, however, that not only does the channel efficiency drop with SNR, but the quasi-optimal modulation scheme also changes. For example, with only 5 dB less SNR (i.e. 25 dB), 256-QAM drops from 2nd to 4th place and 64 QAM emerges as the best conventional modulation scheme. Channel efficiency drops by more than 20% to about 5.5 bps/Hz
  • At 20 dB SNR, 16-QAM yields the best performance, albeit with an additional 30% drop in channel efficiency to about 3.5 bps/Hz.
  • As SNR continues to drop you can see that the quasi-optimal scheme shifts from 16-QAM to 4-QAM (i.e. QPSK) to BPSK.

The figure gives some insight into how the WiFi standards are written around adaptive modulation (i.e. changing schemes depending on SNR - see this note) and why a WiFi network slows down so much when the signal is weak.

Another point to raise here is that there is no theoretical "best" modulation scheme to my knowledge for any given BER and SNR. As a result, designing new modulation schemes has a favorite pastime of communication engineers since at least the 1930's. "Adaptive" schemes like the one shown in the figure are usually some algorithm that selects the best of $N$ available modulation schemes for the SNR measured in the channel. $M$-QAM is somewhat uncomplicated and is therefore used in most benchmarks, but other more exotic modulation schemes can yield marginally better results at the expense of complexity.

AG5CI
  • 542
  • 2
  • 10