How to calculate impedance in antenna design's practice?

Question

I would like to make a match half wave length (λ) dipole antenna (or probably a short dipole antenna). So I would like to make it by measure using LCR meter.

What I am still confuse is about what is the correct formula of impedance (Z). Is in most explanations the formula is written that impedance (Z) = R + jX (Ω), which X is capacitance (and inductance if any). The resistance, the capacitance, and the inductance (if any). As there will be imaginary component there, then the unit will not be ohm (Ω). Then the question is, which one is the correct one for this two formulas (assuming no inductance)?

$$Z = R + jX_C = R + j\frac{1}{2\pi fC} \qquad(1)$$

$$Z = \sqrt{R^2 + (\frac{1}{2\pi fC})^2} \qquad(2)$$

Answer 1

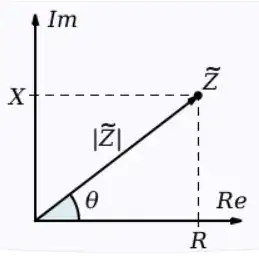
Impedance is the sum of resistance and reactance:

$$ Z = R + jX $$

$j$ is the imaginary unit, equal to $\sqrt{-1}$. Some equations use $i$ instead to mean the same thing.

Reactance is a concept that describes the effects of capacitors and inductors, as well as other components that introduce a phase shift between voltage and current, but don't dissipate energy.

For example, the reactance of a capacitor is given by:

$$ X_C = {-1 \over 2 \pi fC} \tag 1 $$

And for an inductor:

$$ X_L = 2 \pi fL \tag 2 $$

where $C$ is capacitance (farads), $L$ is inductance (henrys), and $f$ is frequency (hertz). From this you can see for capacitors and inductors (and in practice, most other things) the reactance depends on frequency, and capacitors have negative reactance whereas inductors have positive reactance.

The unit of impedance, resistance, and reactance is ohms in each case. Impedance is represented by a complex number, but the unit is still ohms.

---

That's the theory.

In practice, you won't be able to measure the impedance of your antenna with an LCR meter. As you can see in equations 1 and 2, reactance (and thus impedance) depends on frequency. The LCR meter works by measuring the impedance at some frequency, then working backwards though equations 1 or 2 to find the inductance or capacitance.

This works OK for inductors and capacitors (at least, when operating at frequencies where parasitic effects are negligible), but an antenna is something else so equations 1 and 2 don't apply.

Instead, people use an antenna analyzer to measure the impedance directly at the frequency where the antenna is intended to be used.

If you don't have an antenna analyzer, you can use an SWR bridge. This will tell you how close you are to 50 ohms, though not in what direction. There will be a dip in SWR around where the antenna is resonant. Making the antenna longer moves this dip lower in frequency, and making the antenna shorter moves it higher. By measuring SWR at several frequencies and iteratively adjusting the length of the antenna, it's possible to get the antenna to be the right length for the desired frequency.

Answer 2

In general, impedance consists of two parts: a resistive part that dissipates energy and a reactive part that stores energy in an electric or magnetic field. A complex number that includes a real part and an imaginary part is a mathematical tool for keeping track of two related properties of a system. On a Cartesian graph, the real part (resistance) is plotted along the $x$-axis, while the imaginary part (reactance) is plotted along the $y$-axis. By convention, inductive reactance has a positive sign and capacitive reactance has a negative sign. The distance from the origin of the graph to the point $(x,y)$ corresponding to the impedance of interest is the magnitude of the impedance, while the angle of a line segment from the origin to the point is the phase angle of the impedance, as shown in the diagram:

Your first equation should read: $Z=R-j\frac{1}{2\pi fC}$ (note the change of sign). If the reactive part of the impedance was inductive, the equation would be: $Z=R+j2\pi fL$. Your second equation is the magnitude of the impedance: $|Z|=\sqrt{R^2+X^2}$, where $X$ is the inductive or capacitive reactance calculated earlier. The companion of the magnitude of the impedance is its phase angle, which is $arctan\frac{X}{R}$.

Using the simple example of a half-wave dipole, the impedance at the feed point would: be purely resistive at the resonant frequency $(R+j0)$; show capacitive reactance below the resonant frequency $(R-jX_C)$; show inductive reactance above the resonant frequency $(R+jX_L)$. The graph below illustrates this behavior for a half-wave dipole designed for the 20m amateur band (14.1MHz):

Measuring the same dipole's feed point impedance with an $LCR$ meter operating at 100kHz would produce a measurement of $0-j88184 \Omega$, which is equivalent to an 18pF capacitor. Why? At this very low frequency, the 20m dipole is only 0.003 wavelengths long, so it will only radiate (dissipate) a very small amount of energy; thus, the resistive part of the impedance is very small. The capacitive coupling between the two dipole legs dominates the small inductance of the short wires, so the reactance is capacitive.

Answer 3

• Formular (1) is correct for impedance.
  

• Formular (2) calculates the magnitude of Z for e.g. the polar form representation.
  
  

• However with an LCR meter (as in your picture) you won't get the rf impedance of interest for an antenna because the impedance changes considerably between low frequencies (~DC) as measured by an LCR meter and rf frequencies
  
  

• You would need an impedance analyzer or vector network analyzer (VNA) specified for the frequency of interest from your antenna.

• Here are links to 3 youtube videos from w2aew that show an example of such a measurement with the mentioned devices:
  • #282: Part 1: How to measure complex impedance with MFJ-259B | determine sign of X
  • #283: Part 2: Measuring Complex Impedance with MFJ-259B | Crossing the real axis...
  • #264: RF Fun: Visualize antenna tuner operation on Smith Chart, SWR & more with VNA