Why is Euler integration sometimes preferred over RK4 even if RK4 is more accurate?

Question

Some high quality engines such as Box2d uses the Simplistic Euler integrator instead for RK4 when Eumplectic Euler commits a global error of the order of Δt whereas, RK4 has Δtˆ4 error? RK4 is not that hard to do, right? Why would a physics engine use Euler over RK4 hence sacrificing accuracy ?

Answer 1

It's very probable that Erin Cato subtly justified the use of the Symplectic Euler over RK4 or another higher order integrator. The author has lots of slides and/or material (e.g. http://gamedevs.org/uploads/numerical-integration.pdf) related to the inner workings of the Box2D engine. The main reasons for why RK4 is not really needed when writing this kind of a Physics Engine are:

• its improved accuracy is hardly going to make any difference

• it does lose energy, so, a system may seem inherently damped, whereas the Symplectic Euler, although less precise, preserves it (you can simulate stable orbiting motions of satellites around planets without having them crash into the planet)

• it performs approximately 4x the operations needed to update the dynamics in a single step
• in the end, it is not more stable (e.g. even for the simple pendulum equation, the biggest Dt you can take without having things blow up is with the Symplectic Euler) - in games you first need stability, then speed and afterwards you may start thinking about accuracy (and if it's needed at all)

Update

I wrote an academic paper a while ago on how to benchmark and ultimately select the "best" integrator for your needs (http://profs.info.uaic.ro/~jromai/romaijournal/arhiva/2013/2/Cioaca.pdf).

If you want to understand what are the differences between symplectic/energy conserving integrators, explicit and implicit ones, you need to look no further than to how the phase diagrams look like: http://www.acs.psu.edu/drussell/Demos/phase-diagram/phase-diagram.html . For simple oscillators (e.g. the pendulum), these are 2D plots of the angular value against the angular velocity. 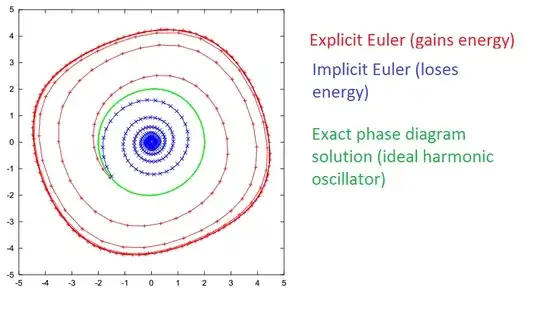If the integrator preserves energy, the phase diagram will basically look like an ellipse, whereas if the integrator loses or gains energy, the phase diagram will resemble a spiral.

Recommended reading

To better understand what's with this stability and symplecticity fuss, one of the best web resources for viewing the effects of these implicit, explicit and semi-implicit integrators is here.

Answer 2

While I can't speak for Erin Catto himself, the simple answer is that in many games-related physics systems a standard Euler method is preferred to a Runge-Kutta method because it is less expensive computationally, while also being sufficiently stable for games in general.

If RK4 was used the integrator would become a larger bottleneck, impacting the potential number of objects that could be simulated on a given system. This may be considered a worse side effect than potential instability when considering this is a library for general application in games.

It's also worth noting that Verlet integration is commonly used as well, especially for fluid/soft-body dynamics. I believe this might be the system used by LiquidFun, which is a fork of Box2D.

At the end of the day these are systems designed to make a product that's fun, not accurate. So, from that perspective, the increased overhead of an RK4 method may not be justifiable in the target use case.

Note: It might be worth considering the history of Box2D. It was originally written as a demonstration for a GDC presentation and thus the integrator chosen may have little to do with it's potential usage as a general library.