Dijkstra and A* are all nice and popular but what kind of algorithm was used in Warcraft 1 for pathfinding?
I remember that the enemy could get trapped in bowl-like caverns which means there were (most probably) no full-path calculations from "start to end". If I recall correctly, the algorithm could be something like this:
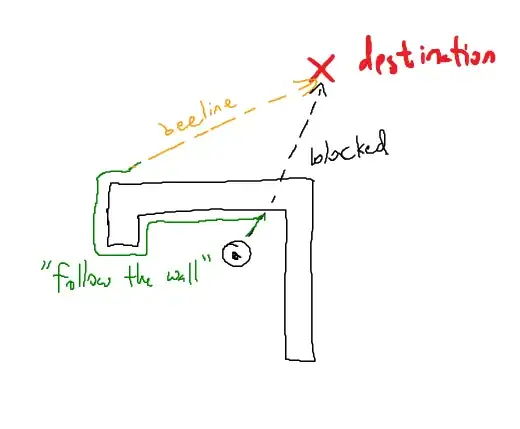
A) Move towards enemy until success or hitting a wall
B) If blocked by a wall, follow the wall until you can move towards the enemy without being blocked and then do A)
But I'd like to know, if someone knows :-)
[edit] As explained to Byte56, I'm searching for a low cpu/mem/mem-bandwidth algo and wanted to know if Warcraft had some special secrets to deliver (never seen that kind of pathfinding elsewhere), I hope that that is more concordant with the stackexchange rules.
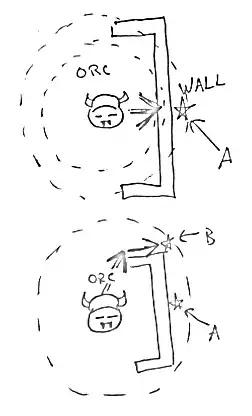
A, ask how you can doA. You're bound to get better answers and it wouldn't be off topic (like this question is). – House Sep 14 '12 at 17:26