How hard to brake to perfectly smoothly reach the destination?

Question

Goal

I want the get the required minimum deceleration to perfectly smoothly reach a target.

(The car's AI should know how hard it has to brake to be the perfect valet.)

Research

• "How can I maneuver an AI pirate ship for a sea battle?" sounds like it might have the answer but I honestly don't understand it, which is why I boiled my question down to be as simple as possible.
• "Max velocity for smooth deceleration to destination" is related but also different
• Physics formula for acceleration, but I don't know if this applies here or not

Conditions

• Solution can be 1D or 2D
• There is no friction
• There is an object o (e.g. car) and a target t (e.g. parking spot)
• Inclusion of object's mass would be nice to have
• The target is static and at a known distance d
• The object has a current known velocity v
• Brake strength is infinite
• No lerping, it should be (somewhat) physically accurate (I later want to add overshoot, impulses, etc.)

Question

What would be the formula to know how hard you had to brake right now to exactly reach 0 velocity at the target?

Answer 1

When an object brakes with a constant deceleration, then its velocity over time looks like this:

Distance traveled is velocity multiplied with time. So the orange area in the graph above actually represents the distance traveled. And the area of a right triangle is half that of a square with the same width and height. So:

$$ distance = (velocity * time) / 2 $$

And the time it takes to get from the current velocity to 0 is the velocity divided by the deceleration, so:

$$ distance = (velocity * velocity / deceleration) / 2 $$

But we know the distance and need the deceleration. So we need to rearrange the formula:

$$ distance * deceleration = (velocity * velocity ) / 2 $$ $$ deceleration = (velocity * velocity ) / ( 2 * distance ) $$

There you have it.

However, this formula assumes that you are using a physics engine that is able to model acceleration by integration. Some physics engines unfortunately just assume that velocities are constant during physics ticks and then changes the velocity between ticks. So in reality the deceleration curve in your engine might actually look like this:

The math still mostly works out over the long term, but can lead to inaccurate results in the short-term. Especially when the engine operates on a variable tick-rate. So if you are using a physics engine that works like that, you might receive results that are "good enough" but not perfectly accurate.

Answer 2

This is a methodology I adopted when designing an automated model train system where the train had to stop at a signal. The physics is much the same as Philipp explains, although I took a slightly different tack to what he describes.

The relevant equation I used was a rearrangement of

distance=(velocity∗velocity/deceleration)/2

Which can be rearranged to give:

velocity*velocity = 2 * distance * deceleration

or

velocity = sqrt(2 * distance * deceleration)

Obviously, you would set this as an upper bound; if your vehicle is travelling less than the target speed (ie a long way from the target), then the vehicle maintains its speed.

Each time I updated the velocity of the train (about 8 times per second) I used that formula to calculate the speed it should be. Since you are allowing acceleration to be infinite, you simply change the velocity by the necessary amount, up to infinity. Any inaccuracies are corrected for in subsequent update steps, so it should converge quite well.

I found this gave a reasonable smooth and realistic-looking stop.

Answer 3

The simpler approach, but still somewhat smooth

By approximation, we could create such a braking curve and this would work for a kind of "smooth" braking:

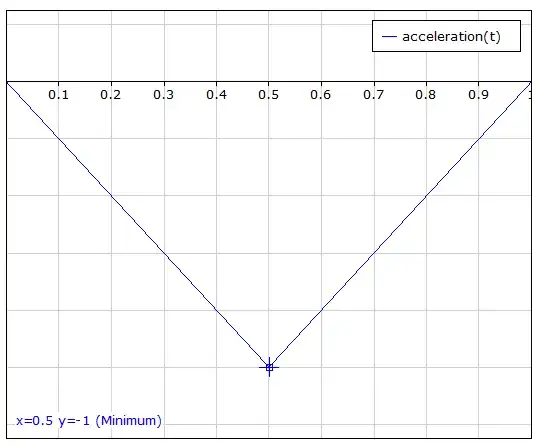
$$ f(t) = \begin{cases} 2t-2, &t \ge \frac{1}{2} \\ -2t, &t < \frac{1}{2} \end{cases} $$

The disadvantage here is that at the kinks \$(0, 0.5, 1)\$ there will be some noticeable not-"smooth"-ness and braking will not be really "smooth"... but it will be almost perfect.

This would be the acceleration with the velocity plotted:

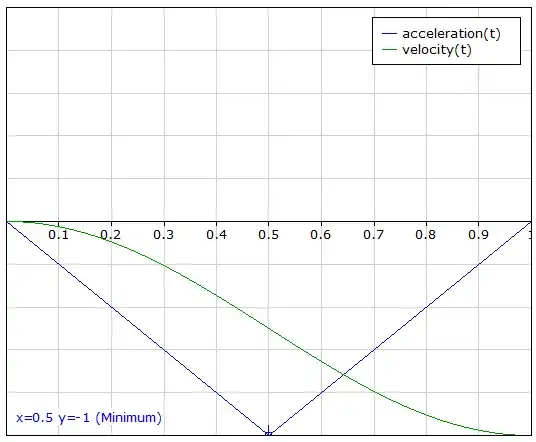
The area of the acceleration for \$t \in [0,1]\$ is easily calculated with the following expression:

$$ v(t) = \frac{cos(\pi t)}{2} - \frac{1}{2} $$

But for the purposes of calculating the maximum deceleration, we know that the "area" (velocity \$v\$) here is equal to \$-1\$ (this function will "remove" this much velocity).

This means that we can just input the velocity as the amplitude when we brake in stop time \$t_{stop}\$.

When the physics engine works by simulating acceleration/deceleration (probably?)

$$ f(t, t_{stop}, v_0) = \begin{cases} k \cdot v_0 \cdot \left(2 \frac{t}{t_{stop}}-2 \right), &\frac{t}{t_{stop}} \ge \frac{1}{2} \\ k \cdot v_0 \cdot \left(-2 \frac{t}{t_{stop}} \right), &\frac{t}{t_{stop}} < \frac{1}{2} \end{cases} $$

where \$v_0\$ is the initial velocity and \$k\$ is some factor.

When the physics engine works by simulating the velocity, not the change in speed

$$ v(t, t_{stop}, v_0) = v_0 + v_0 \cdot \left(\frac{cos \left(\pi \frac{t}{t_{stop}} \right)}{2} - \frac{1}{2} \right) $$

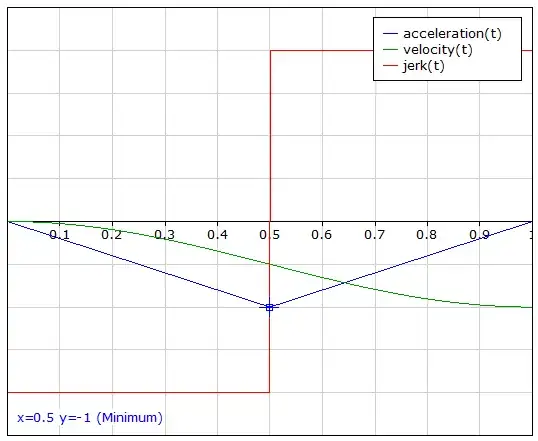
But this will result in jerk, as the "kink" in the graph means the derivative is discontinuous:

The difficult approach, but smooth

If we want smooth braking, I would advise such an acceleration/deceleration curve:

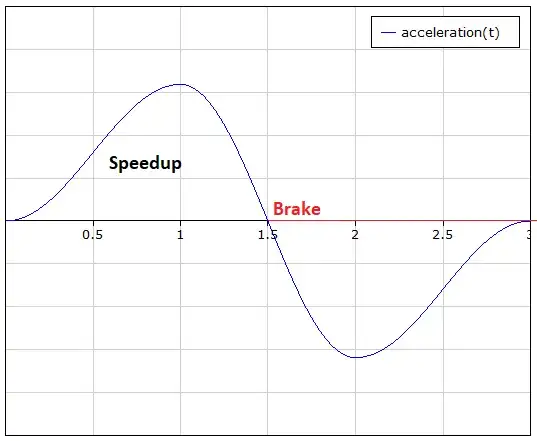
It's not important to know, but this curve consists of three parts (left, middle, right):

$$ f(t) = \begin{cases} \frac{-cos(\pi t)}{\pi} + \frac{1}{\pi}, &t \in [0,1) \qquad(1) \\ \frac{-2cos(\pi t)}{\pi}, &t \in [1,2) \qquad(2) \\ \frac{-cos\pi}{\pi} - \frac{1}{\pi}, &t \in [2,3) \qquad(3) \\ \end{cases} $$

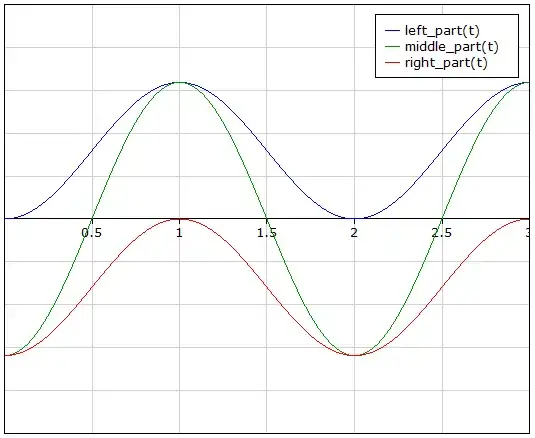
The identified requirements from these three parts start with the first and last parts and consist of:

1. The requirement is a smooth jerkless start.
2. Any kinks in this acceleration/deceleration pattern would introduce jerk.
3. The function must keep decreasing the slope when nearing the zero points.

The middle part is there to just connect the motion into one whole jerkless movement. This would require another chapter in this answer (brake from positive acceleration). For now, I will focus on braking (decelerating) when the acceleration is zero already.

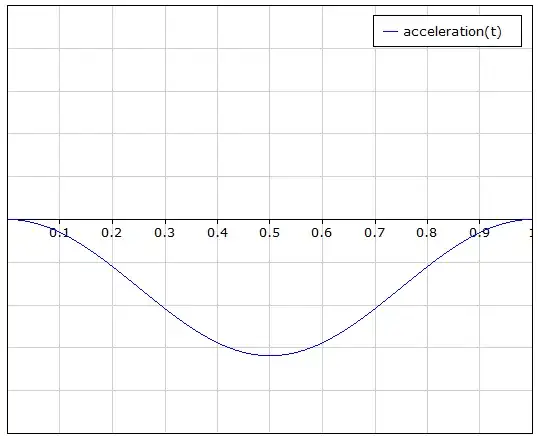
To make this go smoothly, the wanted deceleration curve would approximate this:

It's not important, but the formula used here is

$$f(t) = \frac{-cos(\pi (2t-1))}{\pi} - \frac{1}{\pi}$$

as a basis, to normalize the braking from \$0\$ to \$1\$.

The information we have is:

• The distance \$d\$.
• The current speed \$v\$.

And the question that we have is: what are the parameters (time, amplitude) of the deceleration function, so that the interpolation of that function, equals the speed?

To make this question easier, let's assume that the deceleration curve is calculated, and saved, at one point in time, and is not recalculated.

To make this even easier, let's assign one variable already: time (in how much time we want to stop, stop_time).

Let us just calculate the time from:

$$t_{stop} = \frac{d}{v}$$

We already normalized the brake function for \$t \in [0,1]\$, so we need to divide \$t\$ by the stop time \$t_{stop}\$ to get the curve that fits within the wanted stop time:

$$ f(t, t_{stop}) = \frac{-cos\left(\pi \left(2\left(\frac{t}{stop\_time}\right)-1\right)\right)}{\pi}-\frac{1}{\pi} $$

A car that is going faster obviously needs a higher braking force to stop the same distance (i.e. remove "more" velocity).

To calculate the velocity this function would "remove" we take the integral (from Wolfram Alpha):

$$ \int f(t, t_{stop}) = -\frac{2\left(\frac{t}{2}-\frac{t_{stop} \cdot sin\left(\frac{2 \pi t}{t_{stop}}\right)}{4 \pi}\right)}{\pi} $$

Now, how much velocity does this function remove in total for \$\frac{t}{t_{stop}} = 1\$?

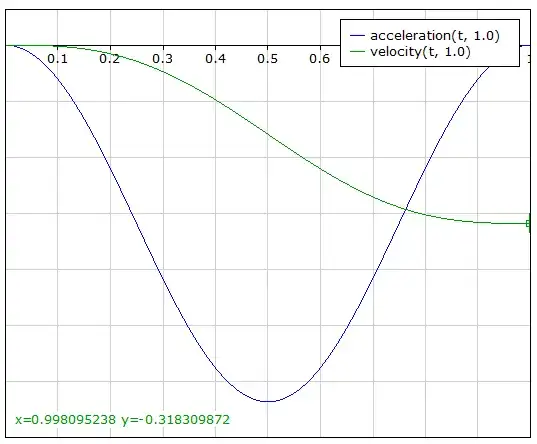
We can see it's around \$\frac{1}{3}\$. Solving it numerically yields \$-\frac{1}{\pi}\$

That's how much velocity this deceleration function is able to remove, so this is our factor for the initial velocity.

For an engine that is velocity-based (already simplified)

$$ v(t, t_{stop}, v_0) = v_0 + v_0 \cdot \left(-2\left(\frac{t}{2}-\frac{t_{stop} \cdot sin\left(\frac{2 \pi t}{t_{stop}}\right)}{4 \pi}\right)\right) $$

Resulting in:

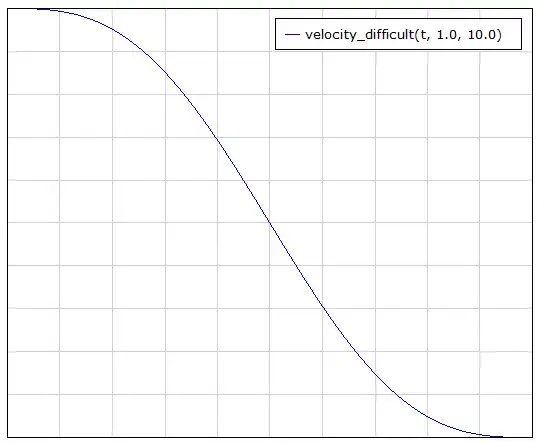
for a stop time \$t_{stop}\$ of 1.0 and initial velocity 10.0.

---

In all formulas, \$t\$ would then be supplied as the time since braking started, and the result can be split into the corresponding x, y, and z components according to the normalized speed vectors of your moving object.