I know the bare minimum to do matrix multiplication and have implemented them from scratch a few times for various purposes, but every time I do, I make sure to be very clear to myself about where are the basis vectors.
I dont think of matrices as big squares of numbers, but as arrays of vectors where each component is.. well, a basis component.
But as I have learned about matrices through alternate means, I have no idea of how this commonly used notation works, and if there's an implicit common sense way to distribute the basis vectors.
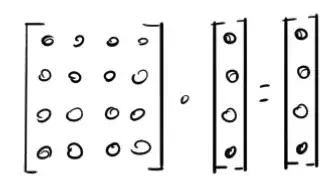
people usually write matrix multiplication in the following notation:
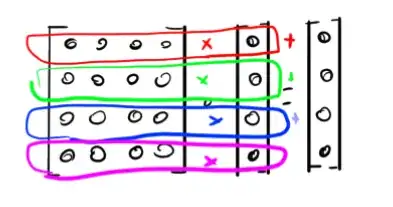
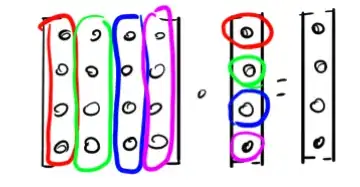
but its very ambiguous to me how to interpret it. my brain is drawn by the visual layout to interpret it as the following:
but most people seem to actually mean this:
so which is the correct way to interpret it?