most efficient AABB vs Ray collision algorithms

Question

Is there a known 'most efficient' algorithm for AABB vs Ray collision detection?

I recently stumbled accross Arvo's AABB vs Sphere collision algorithm, and I am wondering if there is a similarly noteworthy algorithm for this.

One must have condition for this algorithm is that I need to have the option of querying the result for the distance from the ray's origin to the point of collision. having said this, if there is another, faster algorithm which does not return distance, then in addition to posting one that does, also posting that algorithm would be very helpful indeed.

Please also state what the function's return argument is, and how you use it to return distance or a 'no-collision' case. For example, does it have an out parameter for the distance as well as a bool return value? or does it simply return a float with the distance, vs a value of -1 for no collision?

(For those that don't know: AABB = Axis Aligned Bounding Box)

Answer 1

What I have been using earlier in my raytracer:

// r.dir is unit direction vector of ray
dirfrac.x = 1.0f / r.dir.x;
dirfrac.y = 1.0f / r.dir.y;
dirfrac.z = 1.0f / r.dir.z;
// lb is the corner of AABB with minimal coordinates - left bottom, rt is maximal corner
// r.org is origin of ray
float t1 = (lb.x - r.org.x)*dirfrac.x;
float t2 = (rt.x - r.org.x)*dirfrac.x;
float t3 = (lb.y - r.org.y)*dirfrac.y;
float t4 = (rt.y - r.org.y)*dirfrac.y;
float t5 = (lb.z - r.org.z)*dirfrac.z;
float t6 = (rt.z - r.org.z)*dirfrac.z;

float tmin = max(max(min(t1, t2), min(t3, t4)), min(t5, t6));
float tmax = min(min(max(t1, t2), max(t3, t4)), max(t5, t6));

// if tmax < 0, ray (line) is intersecting AABB, but the whole AABB is behind us
if (tmax < 0)
{
    t = tmax;
    return false;
}

// if tmin > tmax, ray doesn't intersect AABB
if (tmin > tmax)
{
    t = tmax;
    return false;
}

t = tmin;
return true;

If this returns true, it's intersecting, if it returns false, it's not intersecting.

If you use the same ray many times, you can precompute dirfrac (only division in whole intersection test). And then it's really fast. And you have also length of ray until intersection (stored in t).

Answer 2

Andrew Woo, who along with John Amanatides developed the raymarching algorithm (DDA) used ubiquitously in raytracers, wrote "Fast Ray-Box Intersection" (alternative source here) which was published in Graphics Gems, 1990, pp. 395-396. Rather than being built specifically for integration through a grid (eg. a voxel volume) as DDA is (see zacharmarz' answer), this algorithm is specifically suited to worlds that are not evenly subdivided, such as your typical polyhedra world found in most 3D games.

The approach provides support for 3D, and optionally does backface culling. The algorithm is derived from the same principles of integration used in DDAs, so it is very quick. More detail can be found in the original Graphics Gems volume (1990).

Many other approaches specifically for Ray-AABB to be found at realtimerendering.com.

EDIT: An alternative, branchless approach -- which would be desirable on both GPU & CPU -- may be found here. The actual code, including the max() on the return test, is available here.

Answer 3

Nobody described the algorithm here, but the Graphics Gems algorithm is simply:

1. Using your ray's direction vector, determine which 3 of the 6 candidate planes would be hit first. If your (unnormalized) ray direction vector is (-1, 1, -1), then the 3 planes that are possible to be hit are +x, -y, and +z.

2. Of the 3 candidate planes, do find the t-value for the intersection for each. Accept the plane that gets the largest t value as being the plane that got hit, and check that the hit is within the box. The diagram in the text makes this clear:

My implementation:

bool AABB::intersects( const Ray& ray )
{
  // EZ cases: if the ray starts inside the box, or ends inside
  // the box, then it definitely hits the box.
  // I'm using this code for ray tracing with an octree,
  // so I needed rays that start and end within an
  // octree node to COUNT as hits.
  // You could modify this test to (ray starts inside and ends outside)
  // to qualify as a hit if you wanted to NOT count totally internal rays
  if( containsIn( ray.startPos ) || containsIn( ray.getEndPoint() ) )
    return true ; 

  // the algorithm says, find 3 t's,
  Vector t ;

  // LARGEST t is the only one we need to test if it's on the face.
  for( int i = 0 ; i < 3 ; i++ )
  {
    if( ray.direction.e[i] > 0 ) // CULL BACK FACE
      t.e[i] = ( min.e[i] - ray.startPos.e[i] ) / ray.direction.e[i] ;
    else
      t.e[i] = ( max.e[i] - ray.startPos.e[i] ) / ray.direction.e[i] ;
  }

  int mi = t.maxIndex() ;
  if( BetweenIn( t.e[mi], 0, ray.length ) )
  {
    Vector pt = ray.at( t.e[mi] ) ;

    // check it's in the box in other 2 dimensions
    int o1 = ( mi + 1 ) % 3 ; // i=0: o1=1, o2=2, i=1: o1=2,o2=0 etc.
    int o2 = ( mi + 2 ) % 3 ;

    return BetweenIn( pt.e[o1], min.e[o1], max.e[o1] ) &&
           BetweenIn( pt.e[o2], min.e[o2], max.e[o2] ) ;
  }

  return false ; // the ray did not hit the box.
}

Answer 4

I'm surprised to see that no one has mentioned the branchless slab method by Tavian

bool intersection(box b, ray r) {
    double tx1 = (b.min.x - r.x0.x)*r.n_inv.x;
    double tx2 = (b.max.x - r.x0.x)*r.n_inv.x;

    double tmin = min(tx1, tx2);
    double tmax = max(tx1, tx2);

    double ty1 = (b.min.y - r.x0.y)*r.n_inv.y;
    double ty2 = (b.max.y - r.x0.y)*r.n_inv.y;

    tmin = max(tmin, min(ty1, ty2));
    tmax = min(tmax, max(ty1, ty2));

    return tmax >= tmin;
}

Full explanation: https://tavianator.com/fast-branchless-raybounding-box-intersections/

Answer 5

Here is an optimized version of the above which I use for GPU:

__device__ float rayBoxIntersect ( float3 rpos, float3 rdir, float3 vmin, float3 vmax )
{
   float t[10];
   t[1] = (vmin.x - rpos.x)/rdir.x;
   t[2] = (vmax.x - rpos.x)/rdir.x;
   t[3] = (vmin.y - rpos.y)/rdir.y;
   t[4] = (vmax.y - rpos.y)/rdir.y;
   t[5] = (vmin.z - rpos.z)/rdir.z;
   t[6] = (vmax.z - rpos.z)/rdir.z;
   t[7] = fmax(fmax(fmin(t[1], t[2]), fmin(t[3], t[4])), fmin(t[5], t[6]));
   t[8] = fmin(fmin(fmax(t[1], t[2]), fmax(t[3], t[4])), fmax(t[5], t[6]));
   t[9] = (t[8] < 0 || t[7] > t[8]) ? NOHIT : t[7];
   return t[9];
}

Answer 6

This is my 3D ray / AABox intersection I've been using:

bool intersectRayAABox2(const Ray &ray, const Box &box, int& tnear, int& tfar)
{
    Vector3d T_1, T_2; // vectors to hold the T-values for every direction
    double t_near = -DBL_MAX; // maximums defined in float.h
    double t_far = DBL_MAX;

    for (int i = 0; i < 3; i++){ //we test slabs in every direction
        if (ray.direction[i] == 0){ // ray parallel to planes in this direction
            if ((ray.origin[i] < box.min[i]) || (ray.origin[i] > box.max[i])) {
                return false; // parallel AND outside box : no intersection possible
            }
        } else { // ray not parallel to planes in this direction
            T_1[i] = (box.min[i] - ray.origin[i]) / ray.direction[i];
            T_2[i] = (box.max[i] - ray.origin[i]) / ray.direction[i];

            if(T_1[i] > T_2[i]){ // we want T_1 to hold values for intersection with near plane
                swap(T_1,T_2);
            }
            if (T_1[i] > t_near){
                t_near = T_1[i];
            }
            if (T_2[i] < t_far){
                t_far = T_2[i];
            }
            if( (t_near > t_far) || (t_far < 0) ){
                return false;
            }
        }
    }
    tnear = t_near; tfar = t_far; // put return values in place
    return true; // if we made it here, there was an intersection - YAY
}

Answer 7

I recently achieved over 61 billion ray/box intersections per second using AVX2 on a Threadripper 3960X (~2 billion single-threaded, ~1.9 cycles per box): https://tavianator.com/2022/ray_box_boundary.html. I don't know what the state of the art is exactly, but that seems like more than enough :)

The unvectorized implementation looks like this. It's a simple implementation of the slab method that handles edge cases:

void intersections(
    const struct ray *ray,
    size_t nboxes,
    const struct box boxes[nboxes],
    float ts[nboxes])
{
    for (size_t i = 0; i < nboxes; ++i) {
        const struct box *box = &boxes[i];
        float tmin = 0.0, tmax = ts[i];
    for (int j = 0; j &lt; 3; ++j) {
        float t1 = (box-&gt;min[j] - ray-&gt;origin[j]) * ray-&gt;dir_inv[j];
        float t2 = (box-&gt;max[j] - ray-&gt;origin[j]) * ray-&gt;dir_inv[j];

        tmin = min(max(t1, tmin), max(t2, tmin));
        tmax = max(min(t1, tmax), min(t2, tmax));
    }

    ts[i] = tmin &lt;= tmax ? tmin : ts[i];
}

}

The vectorized version is similar, packing 8 boxes per struct: https://tavianator.com/2022/ray_box_boundary.html#vectorization

Answer 8

One thing you might want to investigate is rasterizing the front and backfaces of your bounding box in two seperate buffers. Render the x,y,z values as rgb (this works best for a bounding box with one corner at (0,0,0) and the opposite at (1,1,1).

Obviously, this has limited use but I found it great for rendering simple volumes.

For more detail and code:

http://www.daimi.au.dk/~trier/?page_id=98

Answer 9

Here's the Line vs AABB code I've been using:

namespace {
    //Helper function for Line/AABB test.  Tests collision on a single dimension
    //Param:    Start of line, Direction/length of line,
    //          Min value of AABB on plane, Max value of AABB on plane
    //          Enter and Exit "timestamps" of intersection (OUT)
    //Return:   True if there is overlap between Line and AABB, False otherwise
    //Note:     Enter and Exit are used for calculations and are only updated in case of intersection
    bool Line_AABB_1d(float start, float dir, float min, float max, float& enter, float& exit)
    {
        //If the line segment is more of a point, just check if it's within the segment
        if(fabs(dir) < 1.0E-8)
            return (start >= min && start <= max);

        //Find if the lines overlap
        float   ooDir = 1.0f / dir;
        float   t0 = (min - start) * ooDir;
        float   t1 = (max - start) * ooDir;

        //Make sure t0 is the "first" of the intersections
        if(t0 > t1)
            Math::Swap(t0, t1);

        //Check if intervals are disjoint
        if(t0 > exit || t1 < enter)
            return false;

        //Reduce interval based on intersection
        if(t0 > enter)
            enter = t0;
        if(t1 < exit)
            exit = t1;

        return true;
    }
}

//Check collision between a line segment and an AABB
//Param:    Start point of line segement, End point of line segment,
//          One corner of AABB, opposite corner of AABB,
//          Location where line hits the AABB (OUT)
//Return:   True if a collision occurs, False otherwise
//Note:     If no collision occurs, OUT param is not reassigned and is not considered useable
bool CollisionDetection::Line_AABB(const Vector3D& s, const Vector3D& e, const Vector3D& min, const Vector3D& max, Vector3D& hitPoint)
{
    float       enter = 0.0f;
    float       exit = 1.0f;
    Vector3D    dir = e - s;

    //Check each dimension of Line/AABB for intersection
    if(!Line_AABB_1d(s.x, dir.x, min.x, max.x, enter, exit))
        return false;
    if(!Line_AABB_1d(s.y, dir.y, min.y, max.y, enter, exit))
        return false;
    if(!Line_AABB_1d(s.z, dir.z, min.z, max.z, enter, exit))
        return false;

    //If there is intersection on all dimensions, report that point
    hitPoint = s + dir * enter;
    return true;
}

Answer 10

I have added to @zacharmarz answer to handle when the ray origin is inside of the AABB. In this case tmin will be negative and behind the ray so tmax is the first intersection between the ray and AABB.

// r.dir is unit direction vector of ray
dirfrac.x = 1.0f / r.dir.x;
dirfrac.y = 1.0f / r.dir.y;
dirfrac.z = 1.0f / r.dir.z;
// lb is the corner of AABB with minimal coordinates - left bottom, rt is maximal corner
// r.org is origin of ray
float t1 = (lb.x - r.org.x)*dirfrac.x;
float t2 = (rt.x - r.org.x)*dirfrac.x;
float t3 = (lb.y - r.org.y)*dirfrac.y;
float t4 = (rt.y - r.org.y)*dirfrac.y;
float t5 = (lb.z - r.org.z)*dirfrac.z;
float t6 = (rt.z - r.org.z)*dirfrac.z;

float tmin = max(max(min(t1, t2), min(t3, t4)), min(t5, t6));
float tmax = min(min(max(t1, t2), max(t3, t4)), max(t5, t6));

// if tmax < 0, ray (line) is intersecting AABB, but the whole AABB is behind us
if (tmax < 0)
{
    t = tmax;
    return false;
}

// if tmin > tmax, ray doesn't intersect AABB
if (tmin > tmax)
{
    t = tmax;
    return false;
}

// if tmin < 0 then the ray origin is inside of the AABB and tmin is behind the start of the ray so tmax is the first intersection
if(tmin < 0) {
  t = tmax;
} else {
  t = tmin;
}
return true;

Answer 11

This seems similar to the code posted by zacharmarz.
I got this code from the book 'Real-Time Collision Detection' by Christer Ericson under the section '5.3.3 Intersecting Ray or Segment Against Box'

// Where your AABB is defined by left, right, top, bottom

// The direction of the ray
var dx:Number = point2.x - point1.x;
var dy:Number = point2.y - point1.y;

var min:Number = 0;
var max:Number = 1;

var t0:Number;
var t1:Number;

// Left and right sides.
// - If the line is parallel to the y axis.
if(dx == 0){
    if(point1.x < left || point1.x > right) return false;
}
// - Make sure t0 holds the smaller value by checking the direction of the line.
else{
    if(dx > 0){
        t0 = (left - point1.x)/dx;
        t1 = (right - point1.x)/dx;
    }
    else{
        t1 = (left - point1.x)/dx;
        t0 = (right - point1.x)/dx;
    }

    if(t0 > min) min = t0;
    if(t1 < max) max = t1;
    if(min > max || max < 0) return false;
}

// The top and bottom side.
// - If the line is parallel to the x axis.
if(dy == 0){
    if(point1.y < top || point1.y > bottom) return false;
}
// - Make sure t0 holds the smaller value by checking the direction of the line.
else{
    if(dy > 0){
        t0 = (top - point1.y)/dy;
        t1 = (bottom - point1.y)/dy;
    }
    else{
        t1 = (top - point1.y)/dy;
        t0 = (bottom - point1.y)/dy;
    }

    if(t0 > min) min = t0;
    if(t1 < max) max = t1;
    if(min > max || max < 0) return false;
}

// The point of intersection
ix = point1.x + dx * min;
iy = point1.y + dy * min;
return true;

Answer 12

C++ Code

Here is a quasi-branchless and very robust version written in C++:

ray_intersection intersect(vec3 origin, vec3 direction, vec3 box_min, vec3 box_max) {
    vec3 t0 = (box_min - origin) / direction;
    vec3 t1 = (box_max - origin) / direction;
    vec3 min = ray_box_min(t0, t1); // entry points per plane
    vec3 max = ray_box_max(t0, t1); // exit points per plane
    double t_min = std::fmax(std::fmax(min.x, min.y), min.z);
    double t_max = std::fmin(std::fmin(max.x, max.y), max.z);
    return { t_min, t_max };
}

This also requires the use of two utility functions:

double ray_box_min(double x, double y) {
    return std::isnan(x) || std::isnan(y) ? -inf : std::fmin(x, y);
}
double ray_box_max(double x, double y) {
    return std::isnan(x) || std::isnan(y) ? +inf : std::fmax(x, y);
}
vec3 ray_box_min(vec3 a, vec3 b) {
    return { ray_box_min(a.x, b.x), ray_box_min(a.y, b.y), ray_box_min(a.z, b.z) };
}
vec3 ray_box_max(vec3 a, vec3 b) {
    return { ray_box_max(a.x, b.x), ray_box_max(a.y, b.y), ray_box_max(a.z, b.z) };
}

Explanation

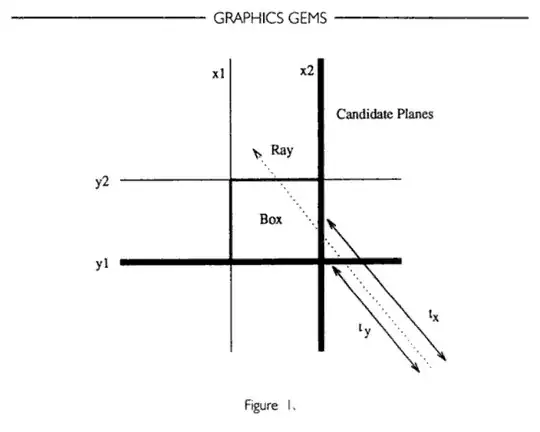
This implements the well-known Slab method.

All operations including / and min/max are component-wise when applied to vectors in this code.

We cannot use regular std::fmin but must use a custom ray_box_min for numerical stability. If the ray origin is inside a box plane and the ray direction is parallel to the box plane, the first division yields NaN. We replace this with -inf and +inf depending on the operation. This results in the value getting replaced by others when computing t_min or t_max.

If you can guarantee that the ray origin is outside the box, you can use a regular component-wise min and max instead of the ray_box_ variants.

Interpreting the results

• t_min is the furthest entry point
• t_max is the closest exit point

From these values, we can obtain all sorts of properties:

• If t_min <= t_max, the intersection is not a miss.
  • If also t_min > 0, the intersection is completely in front.
  • If also t_max < 1, the intersection is completely behind.
    • If also t_min < 0 && t_max > 0, the ray origin is inside the box.
• If t_min is NaN or t_max is NaN, the ray direction is the zero-vector.
• If t_min == 0, the ray origin lies on the box surface.
• If t_min == t_max, the box has no volume, or an edge or corner was hit. Either way, the intersection is a single point, not a line segment.