How to adapt pathfinding algorithms to restricted movement?

Question

Imagine car-like movement where entities cannot turn on a dime. Say, for the sake of discussion, that when at-speed they can turn 90 degrees per second. This would in many cases change the optimal path and therefore the pathfinding. It may even make 'usual' paths entirely impossible to traverse.

Are there any pathfinding algorithms or movement planning algorithms that can keep this in mind, or are there simple ways to adapt the popular ones?

Answer 1

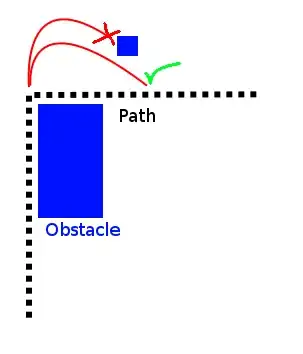
Welcome to the wonderful world of non-holonomic motion planning. I recommend doing this using a lattice grid path planner. Other alternatives include the kinodynamic RRT, and trajectory optimization. Non-holonomic systems include cars, boats, unicycles, or really anything where the vehicle can't travel in any direction it wants. Planning for these systems is much harder than holonomic systems and until ~2000 was on the edge of academic research. Nowadays there are lots of algorithms to choose from which work decently.

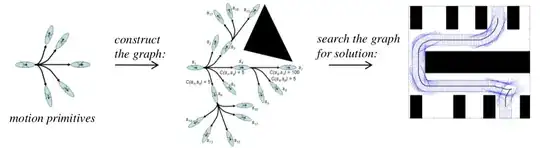
Here's how it works.

State

Your car's configuration q is actually a 3D state containing the car's x, y position and its orientation t. The nodes in your A* algorithm are actually 3D vectors.

class Node
{
    // The position and orientation of the car.
    float x, y, theta;
}

Actions

So what about the edges?

That's slightly harder, because your car could actually choose an infinite number of ways to turn the wheel. So, we can make this accessible to a lattice grid planner by restricting the number of actions the car can take to a discrete set, A. For the sake of simplicity lets assume that the car doesn't accelerate but rather can change its velocity instantaneously. In our case, A can be as follows:

class Action
{
    // The direction of the steering wheel.
    float wheelDirection;

    // The speed to go at in m/s.
    float speed;

    // The time that it takes to complete an action in seconds.
    float dt;
}

Now, we can create a discrete set of actions that the car can take at any time. For example, a hard right while pressing the gas at full for 0.5 seconds would look like this:

Action turnRight;
turnRight.speed = 1;
turnRight.wheelDirection = 1;
turnRight.dt = 0.5;

Putting the car into reverse and backing up would look like this:

Action reverse;
reverse.speed = -1;
reverse.wheelDirection = 0;
reverse.dt = 0.5;

And your list of actions would look like this:

List<Action> actions = { turnRight, turnLeft, goStraight, reverse ...}

You also need a way of defining how an action taken at a node results in a new node. This is called the forward dynamics of the system.

// These forward dynamics are for a dubin's car that can change its
// course instantaneously.
Node forwardIntegrate(Node start, Action action) 
{
    // the speed of the car in theta, x and y.
    float thetaDot = action.wheelDirection * TURNING_RADIUS;

    // the discrete timestep in seconds that we integrate at.
    float timestep = 0.001;

    float x = start.x;
    float y = start.y;
    float theta = start.theta;

    // Discrete Euler integration over the length of the action.
    for (float t = 0; t < action.dt; t += timestep)
    {
       theta += timestep * thetaDot;
       float xDot = action.speed * cos(theta);
       float yDot = action.speed * sin(theta);
       x += timestep * xDot;
       y += timestep * yDot;
    }

    return Node(x, y, theta);
}

Discrete Grid Cells

Now, to construct the lattice grid, all we need to do is hash the states of the car into discrete grid cells. This turns them into discrete nodes that can be followed by A*. This is super-important because otherwise A* would have no way of knowing whether two car states are actually the same in order to compare them. By hashing to integer grid cell values, this becomes trivial.

GridCell hashNode(Node node)
{
    GridCell cell;
    cell.x = round(node.x / X_RESOLUTION);
    cell.y = round(node.y / Y_RESOLUTION);
    cell.theta = round(node.theta / THETA_RESOLUTION);
    return cell; 
}

Now, we can do an A* plan where GridCells are the nodes, Actions are the edges between nodes, and the Start and Goal are expressed in terms of GridCells. The Heuristic between two GridCells is the distance in x and y plus the angular distance in theta.

Following the Path

Now that we have a path in terms of GridCells and Actions between them, we can write a path follower for the car. Since the grid cells are discrete, the car would jump inbetween cells. So we will have to smooth out the motion of the car along the path. If your game is using a physics engine, this can be accomplished by writing a steering controller that tries to keep the car as close as possible to the path. Otherwise, you can animate the path using bezier curves or simply by averaging the nearest few points in the path.

Answer 2

Most path finding algorithms work on a arbitrary graph without restriction of geometry.

So what you need to do is add orientation of the car to each explored node and restrict which nodes are actually connected.

Answer 3

My thoughts, havent tested them!

1. Run A* from start to destination, return the path.
2. Loop through the path, when you detect a turn, use a bezier algorithm (or any like it) which uses the seekers current speed to predict the nodes that will create a smooth turn. Make sure it tries to go back to the closest path-node.
3. If the turn can be done, great, if not, repeat with slower speed, making for a sharper turn.
4. Once the correct path is created, go back through the path adjusting the speed of the seeker before the turn is made so it slows down to the correct speed before it initiates the turn.
5. If the turn cannot be made at all, run the whole thing again. Just ensure all the handled nodes of the turn that cannot be made are in the closed list, so they are ignored. And you could start with the point where the turn is initiated so you can skip the succesfull part of the path, however, in some cases this could possibly result in a less than optimal path.

You should also be able to do this without having to complete the path first, ergo: handling turns during A*, which will probably be much better optimized, but it might also prove to be problematic and glitchy, i really wouldnt know and unfortunatly i dont have the time to test it myself.

Answer 4

If your agent has full control of the car, do it the other way around. Connect a line from start to finish first, then figure out at what speed you can navigate each turn, similar to Dennis's answer.

Don't draw Bezier curves from fixed points though. To minimize speed loss you need to move the entire line around, so start by inserting extra nodes at more or less even distance and then move then for energy minimization or similar strategies. For details you need to look into AI line generation in (preferably sim or semi-sim) racing games.

Once you have the AI line system running, run your A* search and for each path go at least one corner forward, then calculate the AI line which gives you a time estimation. This would be your cost function.