I'm not entirely sure I get what you are asking, but here goes.
Mathematically all rotations happen around the origin. So if you want to rotate something around a different point, you'd move it so that the difference from the origin is the same as it would be from that point and then moving it back by the same amount.
Now I think what you are asking is how to rotate one point smoothly so that it ends up on another specific point. Let's call the first point a and the second point b.
You first need to pick a point that has the same distance from both of them.
If you are in 2D you can pick any point like this:
//t is some arbitrary value
x=(a.x+b.x)/2+t*(b.y-a.y);
y=(a.y+b.y)/2-t*(b.x-a.x);
p=new Vector(x,y);
In 3D it's slightly more complicated, but you can always find a plane that goes through both points and treat it like it's a 2D problem.
Now if you have your point p that you want to rotate around, you need to figure out the angles here. That's where the atan2 function is super helpful. It tells you the angle that a 2d vector has relative to the positive x axis.
So you get:
startAngle = atan2(a-p);
endAngle = atan2(b-p);
Now you can smoothly rotate from a to b. (Note that you will always rotate counter clockwise if you do this naively, so check if clockwise is faster)
Be advised that you want to figure out how fast to rotate depending on the length of the ark. So you basically want to divide your rotation speed by 2*pi*length(a-p).
Now with all that being said:
If you want to make tracking rockets this is a bad way to go about it.
I think what you actually want is to shoot the tracking rocket in a direction that is slightly off target and let it slowly correct it's path. Potentially allow it to change it's direction faster over time or something. That way your rocket will react much more naturally to for example an enemy spaceship moving after it's been fired instead of looking like it's been glued to an invisible ark attached to the spaceship.
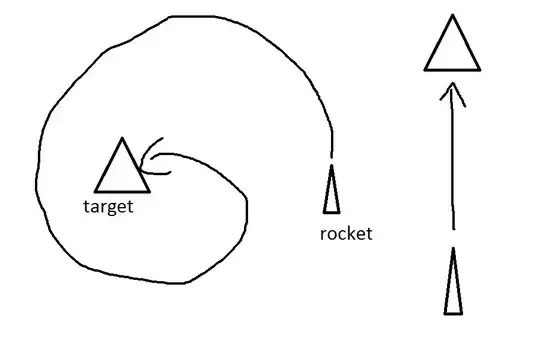 The reason for this is that I want to implement a homing lethargic missile.
The reason for this is that I want to implement a homing lethargic missile.