Looking for an easing equation

Question

I am looking for an easing equation with the following properties:

It starts at a velocity of zero, and eases into a constant velocity of 1 for a duration of t_1 seconds (cubic, exp, or quintic, doesn't matter)
It then has a constant velocity of 1 for t_2 seconds.
Finally, it eases down to zero velocity for a period of t_3 seconds.
t_1 + t_2 + t_3 = t_max
The function starts at zero and ends at 1.
t_2 will be chosen by the easing function to satisfy (4) and (5), given t_1, t_3, and t_max.

Therefore the function has the form:

float EaseConstantVelocity(float current_time, float t_1, float t_3, float t_max)
{
    // ?
}

How do I construct such an easing function?

Edit:

What I'm looking for is conceptually similar to the CubicInOut function, except in the case of CubicInOut, t_2 is 0.

Have you seen this post? http://gamedev.stackexchange.com/questions/6978/easing-functions?rq=1 Or all these? http://gamedev.stackexchange.com/questions/tagged/easing — House, Jun 15 '15 at 20:53
Yes, I guess the answer is just to understand the easing functions. — mklingen, Jun 15 '15 at 20:55
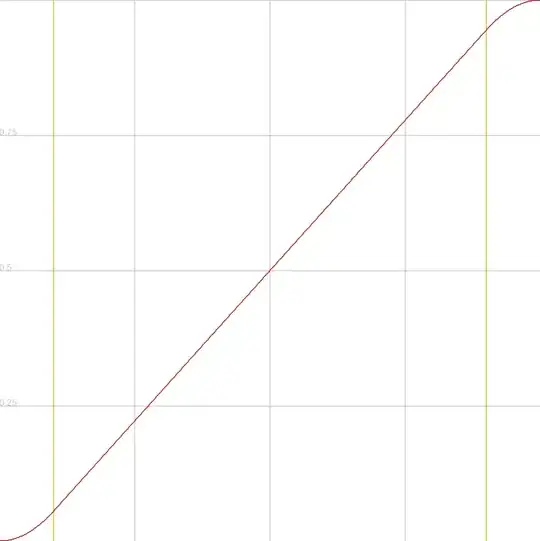
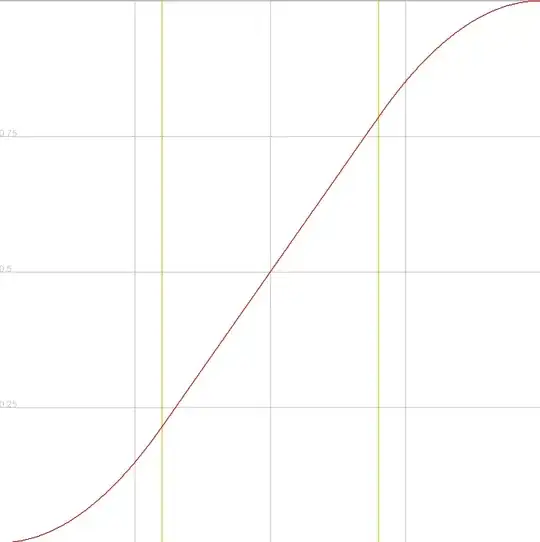
Hmm, I think what I want can be found by tweaking SMOOTHSTEP into a piecewise equation — mklingen, Jun 15 '15 at 21:01
Your constraints might not always be satisfiable. Eg. if the input is such that t_max - t_1 - t_3 > 1, then a constant velocity of 1 over time t_2 will result in the function increasing in value by more than 1, so it would have to go backwards in the t_1 or t_3 periods (you haven't explicitly stated that this isn't allowed, but I'm guessing it's undesireable) in order to hit the described endpoints of 0 and 1. Instead, would you want just some constant velocity during the middle segment, whether it's 1 or some other constant? — DMGregory, Jun 15 '15 at 21:05
@DmGregory, you're right! I've solved the problem based on this suggestion. I'll post my solution. — mklingen, Jun 16 '15 at 00:33

mklingen · Accepted Answer · 2015-06-16T16:01:20.253

As @DMGregory pointed out, it isn't satisfiable when the constant velocity desired is 1. As t_1 and t_3 grow in size, a constant velocity of 1 will not cause the linear segment to reach t_max in time. Therefore, a correction factor has to be applied to allow the slope to change to support this. Here's the code I used to accomplish what I wanted:

// Some initialization. t_1 and t_max can be varied, the other parameters are fixed.
float t_1 = 0.1;
float t_3 = t_1;
float t_max = 1.0;
float t_2 = t_max - (t_1 + t_3);


// Equations for each of the segments
// The first segment is a quadratic which levels off at velocity 1 when t = t_1.
float f1(float t)
{
  return (1.0f / (2 * t_1)) * pow(t, 2.0f);
}
// The second segment is linear with velocity 1, and begins at f(t_1).
float f2(float t)
{
  return  t + f1(t_1) - t_1;
}
// The third segment is quadratic, with initial velocity 1 and final velocity 0.
float f3(float t)
{
  return f2(t_1 + t_2) -  (1.0f / (2.0f * t_3)) * (pow(t_max - t, 2.0f)) + 0.5 * t_3;
}

// The final easing function is a piecewise combination of the others
float easing(float t)
{
  // This is a correction that forces the easing function to end at 
  // t_max. The whole function is multiplied by this.
  float correction = (t_max/ (t_max- t_1));

  // Piecewise elements
  if (t < t_1)
  {
    return correction * f1(t);
  } 
  else if(t < t_1 + t_2)
  {
    return correction * f2(t);
  }
  else if(t < t_max)
  {
    return correction * f3(t); 
  }
  else
  {
    return t_max; 
  }
}

And here are some plots for different values of t_1. Imgur Imgur Imgur

Looking for an easing equation

1 Answers1