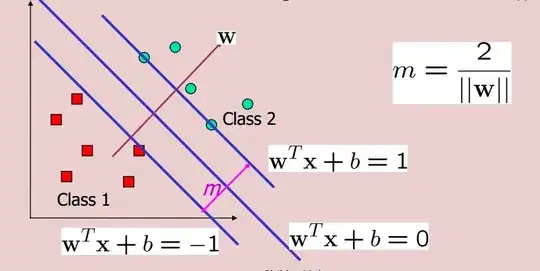
While using support vector machines (SVM), we encounter 3 types of lines (for a 2D case). One is the decision boundary and the other 2 are margins:
Why do we use $+1$ and $-1$ as the values after the $=$ sign while writing the equations for the SVM margins? What's so special about $1$ in this case?
For example, if $x$ and $y$ are two features then the decision boundary is: $ax+by+c=0$. Why are the two marginal boundaries represented as $ax+by+c=+1$ and $ax+by+c=-1$?