How many parameters does a single stacked LSTM have? The number of parameters imposes a lower bound on the number of training examples required and also influences the training time. Hence knowing the number of parameters is useful for training models using LSTMs.
5 Answers
The LSTM has a set of 2 matrices: U and W for each of the (3) gates. The (.) in the diagram indicates multiplication of these matrices with the input $x$ and output $h$.
- U has dimensions $n \times m$
- W has dimensions $n \times n$
- there is a different set of these matrices for each of the three gates(like $U_{forget}$ for the forget gate etc.)
- there is another set of these matrices for updating the cell state S
- on top of the mentioned matrices, you need to count the biases (not in the picture)
Hence total # parameters = $4(nm+n^{2} + n)$
- 631
- 7
- 14
- 1,297
- 2
- 12
- 15
Following previous answers, The number of parameters of LSTM, taking input vectors of size $m$ and giving output vectors of size $n$ is:
$$4(nm+n^2)$$
However in case your LSTM includes bias vectors, (this is the default in keras for example), the number becomes:
$$4(nm+n^2 + n)$$
- 1,783
- 11
- 22
- 34
- 1,083
- 7
- 10
-
3This is the only complete answer. Every other answer appears content to ignore the case of bias neurons. – Feb 07 '18 at 14:11
-
2To give a concrete example, if your input has m=25 dimensions and you use an LSTM layer with n=100 units, then number of params = 4(10025 + 100**2 + 100) = 50400. – arun Jun 20 '18 at 00:13
-
1Suppose I am using timestep data, is my understanding below correct? n=100: mean I will have 100 timestep in each sample(example) so I need 100 units. m=25 mean at each timestep, I have 25 features like [weight, height, age ...]. – jason zhang Mar 10 '19 at 06:41
-
4@jasonzhang The number of timesteps is not relevant, because the same LSTM cell will be applied recursively to your input vectors (one vector for each timestep). what arun called "units" is also the size of each output vector, not the number of timesteps. – Adam Oudad Mar 11 '19 at 08:24
According to this:
LSTM cell structure
LSTM equations
Ingoring non-linearities
If the input x_t is of size n×1, and there are d memory cells, then the size of each of W∗ and U∗ is d×n, and d×d resp. The size of W will then be 4d×(n+d). Note that each one of the dd memory cells has its own weights W∗ and U∗, and that the only time memory cell values are shared with other LSTM units is during the product with U∗.
Thanks to Arun Mallya for great presentation.
- 383
- 3
- 6
to completely receive you'r answer and to have a good insight visit : https://towardsdatascience.com/counting-no-of-parameters-in-deep-learning-models-by-hand-8f1716241889
g, no. of FFNNs in a unit (RNN has 1, GRU has 3, LSTM has 4)
h, size of hidden units
i, dimension/size of input
Since every FFNN(feed forward neural network) has h(h+i) + h parameters, we have
num_params = g × [h(h+i) + h]
Example 2.1: LSTM with 2 hidden units and input dimension 3.
g = 4 (LSTM has 4 FFNNs)
h = 2
i = 3
num_params
= g × [h(h+i) + h]
= 4 × [2(2+3) + 2]
= 48
input = Input((None, 3))
lstm = LSTM(2)(input)
model = Model(input, lstm)
thanks to RAIMI KARIM
- 61
- 1
- 3
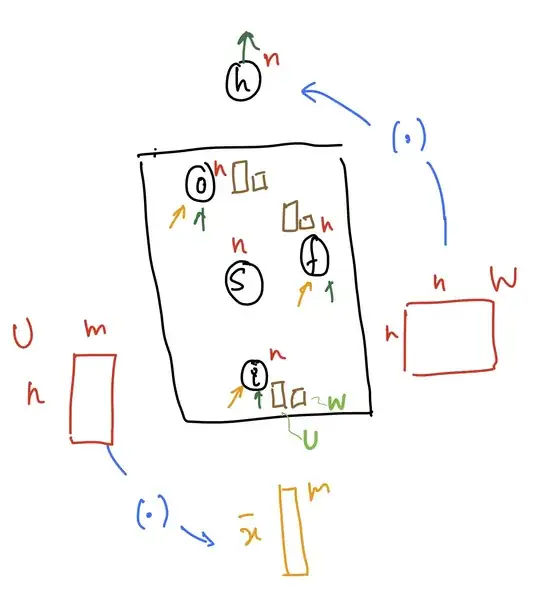
To make it clearer , I annotate the diagram from http://colah.github.io/posts/2015-08-Understanding-LSTMs/.
ot-1 : previous output , dimension , n (to be exact, last dimension's units is n )
i: input , dimension , m
fg: forget gate
ig: input gate
update: update gate
og: output gate
Since at each gate, the dimension is n, so for ot-1 and i to get to each gate by matrix multiplication(dot product), need nn+mn parameters, plus n bias .so total is 4(nn+mn+n).
- 111
- 2


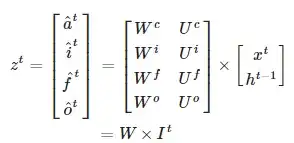


PS: I didn't answer my own question to just gain reputation points. I want to know if my answer is right from the community. – wabbit Mar 09 '16 at 11:17