Proving this language is not context free using the pumping lemma

Question

I am trying to prove why the below language is not context free. Note: this should be carried out by applying the pumping lemma for context free languages.

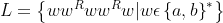
$L = \left \{ ww^{R}ww^{R}w |w\epsilon \left \{ a,b \right \}^{*} \right \}$

To prove something with the pumping lemma, we firstly need to choose an arbitrary m > 0. After that we need to formulate the string (alpha below) we are going to reach a contradiction with. But how do I formulate that string? Rational thinking lead me to believe it's the following:

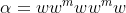
$\alpha = ww^{m}ww^{m}w$

What do I do next?
I have no idea about the length of $w$, and therefore the above approach seems kind of useless.

Is the solution to constrain $w$ to be of length at most $m$?
But again, I wouldn't know what to do from there.

Welcome to Computer Science! Note that you can use LaTeX here to typeset mathematics in a more readable way. See here for a short introduction. — Raphael, Aug 10 '17 at 19:09
You may want to check out our reference question. Duplicate? — Raphael, Aug 10 '17 at 19:09
Note that you can include LaTeX directly into your posts by using $...$ and $$...$$. There's no need to link to third-party sites that render LaTeX as images. — David Richerby, Aug 11 '17 at 09:30

score 1 · Accepted Answer · answered Aug 10 '17 at 22:00

Here in the notation of the language superscript $R$ is not a number; you cannot choose it to be a length $m$.

Instead $R$ usually denotes the operation of "mirror image" which inverts a string: $(abbaa)^R = aabba$.

Now start rereading your notes on the Pumping Lemma.

Proving this language is not context free using the pumping lemma

1 Answers1