Order of various functions

Question

I am to arrange the following 30 functions in terms of increasing order
( all the lg (log) are to the base 2.
log* represents iterated logarithm.)

Here's my answer (the functions on the same level are of the same order):

1 , 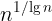$\large n^{1/{\lg n}}$

lglg*n

lg*n,      lg*(lgn)

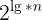
$\large 2^{\lg*n}$

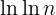
$\large \ln\ln n$

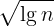
$\large \sqrt{\lg n}$

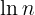
$\large \ln n$

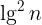
$\large \lg^{2} n$

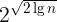
$\large \2^{\sqrt{2\lg n}}$

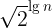
$\large \sqrt{2}^{\lg n}$

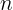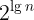
$\large n$ , $\large 2^{\lg n}$

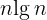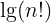
$\large n{\lg n}$ , $\large {\lg (n!)}$

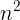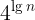
$\large n^{2}$ , $\large 4^{\lg n}$

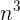
$\large n^3$

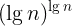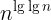
$\large (\lg n)^{\lg n}$ , $\large n^{\lg \lg n}$

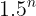
$\large 1.5^n$

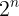
$\large 2^n$

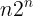
$\large n2^n$

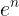
$\large e^n$

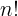
$\large n!$

$\large (n+1)!$

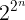
$\large 2^{2^{n}}$

$\large 2^{2^{n+1}}$

I am not sure where to insert (logn)!. I know (logn)! = o((logn)^logn) and logn = o((logn)!), isn't it. But where exactly would it fit. Can anyone help me with that. Also I would really appreciate if someone could verify that my arrangement is right or not.

Thank you.

EDIT : I MEANT TO ASK THE POINT OF INSERTION OF (LOGN)! IN THE ABOVE LIST SORTED IN TERMS OF INCREASING ORDER. Simple.

Could you use LaTeX instead of pictures? It may happen that you do not know order of some element - it is a good potential question about that particular element, but I bet that you have no problem with $n, n^2, n^3, 2^n$. I mean that the whole excersise is not proper question, but also you do not need feedback to all of them. Trimming down the question would point to the source of the confusion. — Evil, Sep 18 '16 at 16:06
@Evil, roger that mate, I just listed it all out just hoping that if there's some mistake in the entire arrangement then someone might point it out. — ps_, Sep 18 '16 at 16:26
Possible duplicate of Sorting functions by asymptotic growth — David Richerby, Sep 18 '16 at 17:59

score 2 · Answer 1 · answered Sep 18 '16 at 16:01

2

Stirling's formula asserts that $$ n! = \Theta(\sqrt{n}(n/e)^n). $$ Thus $$ (\log n)! = \Theta(\sqrt{\log n}((\log n)/e)^{\log n}). $$

answered Sep 18 '16 at 16:01

Yuval Filmus

276,994
27
311
503

That still doesn't answer the question. The set needs a complete ordering. Where in the list would should that function be placed. I was able to use Stirling's formula to deduce (logn)! = o((logn)^logn). – ps_ Sep 18 '16 at 16:33

Order of various functions

1 Answers1