4

I've spent the last hours trying to come up with an algorithm that shuffles an ordered set of numbers (i.e a simple range of numbers) in a way that I can retrieve from a shuffled value the original value that was on that position without the need to store all relationships between shuffled values and their counterparts.

The statement above may not make any sense to you, but I've learned some terms while trying to find such algorithm that may help me to describe what I mean...

First of all I believe that this algorithm/function is bijective, which means it is deterministic and one member of $A$ has only one correspondent member of $B$ and vice-versa:

            

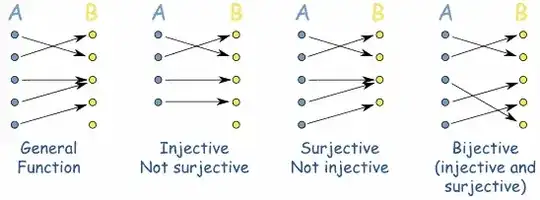
Another peculiarity is that input and output domains are exactly the same so, following the above example, $A$ = $B$ = $D$ with $D$ being a range from $m$ to $n$.

To sum everything up (sorry I'm pretending that I know math):

$D = \{x \in \mathbb N\ | m \le x \le n \}$

$ \forall x \in D \land \forall y \in D\\ f(x) = y \implies \exists g(y) = x $

What could be done to simply implement $f$ and $g$ ?

The closest solutions I've found are some kind of block cipher which I'm unable understand nor tweak to achieve the desired behavior which is much simpler.

As one last attempt to explain this, here is a simple use case:

  • Consider integer codes that can range from 1 to 2^31
  • On the backend these codes are used sequentially, getting increased one by one
  • Instead of sending one of these codes for a client, our function picks another code from that range to represent the original one
  • Despite we need to use those codes sequentially we are only sending the random values for the clients so it looks random from his perspective
  • When we receive this code back the from the client we're able to tell the original code
  • We would also be able to change the way that these codes are "shuffled", so different codes could be exposed over time while leaving the original ones untouched on our side

Sorry if I wasn't clear enough or destroyed math notations forever.

Community
  • 1
cvsguimaraes
  • 143
  • 5
  • So basically you're looking for any bijective function $f : A \mapsto B$? Do you want it to be hard for the client to decypher the code? Then RSA is probably something you want to look at. – Auberon Apr 11 '16 at 09:29
  • Perhaps you need a trapdoor function? Or maybe a public key encryption scheme? – Jay Apr 11 '16 at 09:51
  • "retrieve from a shuffled value the original value that was on that position without the need to store all relationships between shuffled values and their counterparts" -- that immediately triggers a voice saying "a simple adversary argument shows that it's impossible" in my head. – Raphael Apr 11 '16 at 10:11
  • What exactly do you mean by "shuffle"? The term is used in CS to mean "reorder to a uniformly random permutation". Is that what yo mean, or do you want just some reordering? – Raphael Apr 11 '16 at 10:12
  • Lastly, using any kind of cipher is probably more expensive than just storing the old array, if it works at all. – Raphael Apr 11 '16 at 10:13
  • The title you have chosen is not well suited to representing your question. Please take some time to improve it; we have collected some advice here. Thank you! – Raphael Apr 11 '16 at 10:13

1 Answers1

5

The subject is called format-preserving encryption,
and your last bullet point is addressed by tweaks.

Simple
http://web.cs.ucdavis.edu/~rogaway/papers/feistel.pdf
http://arxiv.org/pdf/1208.1176.pdf
http://web.cs.ucdavis.edu/~rogaway/papers/sr.html
Complex