tightest upper bound on binary search tree insertion?

Question

The upper bound on the runtime of binary search tree insertion algorithm is O(n) which is if it is not balanced What will be the tighter upper bound on this,will it become O(logn) I have read that tighter upper and lower bounds are often equivalent to the Theta notation.

Answer 1

For a binary search tree of $n$ nodes ,

Maximum height $=h_{max}=n-1 = \Theta (n) =O(n)$

which happens in the case of skewed binary search tree as below if all elements of a binary search are either right-skewed or left-skewed

So in worse case , to add a new node in to an existing skewed binary search tree , it takes $n$ comparisons (comparison at each level).

So, time taken $= h_{max}+1=n=\Theta\ O(n)$

---

Minimum height = $h_{min}=\lceil \log_2{(n+1)}\rceil-1=\Theta(\log(n))=O(\log(n))$

which happens in the case of complete binary search tree as below if all levels contains all elements except last level (Last level may be not contain all elements).

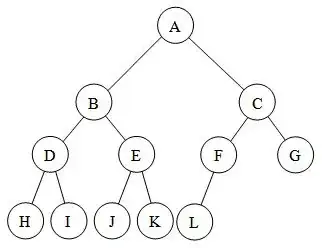
Now, number of comparisons $= h_{min}+1=\lceil \log_2{(n+1)}\rceil=\Theta(\log(n))=\ O(\log_2(n))$

Which may be the tightest upper bound you are asking for .

So, you can use either $\Theta$ or $\ O$ notation here. $\Theta$ is tighter .

Whenever you use $\Theta$ you can replace it with $\ O$ but not viceversa .