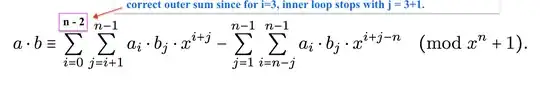May someone please explain how the reduction is done? I am familiar with other algebraic structures but wondering if I am doing reduction correctly for this.
It is understood that a Polynomial Ring of this form, $\mathbb{Z}_{q}[x]/(x^n + 1)$, consists of the set of all polynomials defined by $(x^n + 1)$ with coefficients over $\mathbb{Z}_q = \{0, 1, ..., q-1\}$.
For simplicity, say I am working in $\mathbb{Z}_{5}[x]/[x^4+1]$
Say I multiply two polynomials in the ring according to the convolution formula.
3 2 1 0 <-- coefficient indecis
$a(x) = 4x^3 + 1x^2 + 1x + 2$
$b(x) = 1x^3 + 1x^2 + 3x + 2$
$n=4, n-1=3$
all coefficient arithmetic is done mod 5 add like terms and reduce mod 5 negative numbers, we add multiples of mod 5
$$a(x)\cdot b(x) = ([(a_0b_1x + a_0b_2x^2 + a_0b_3x^3) + (a_1b_2x^3 + a_1b_3x^4 + a_2b_3x^3)] - \\ [a_3b_1 + a_2b_2 + a_3b_2x + a_1b_3 + a_2b_3x + a_3b_3x^2]) \mod (x^4 + 1)\\ =[(x + 2x^2 + x^3) + (x^3 + x^4 + x^3)] - [(2 + 1 + 4x + 1 + 1x + 4x^2)] \mod.. \\ = [x^4 + 3x^3 + 2x^2 + x] - [4x^2 + 4] \mod..\\ = [x^4 + 3x^3 + (2-4)x^2 + x - 4] \mod..\\ = [x^4 + 3x^3 + 3x^2 + x + 1] \mod (x^4 + 1) $$
Three questions:
- convolution formula is correct.
- subtraction is like normal polynomials: $4x^2 - x^2 = 3x^2$
- reduction: done like standard polynomial division to obtain residue
Given $(x^4 + 3x^3 + 3x^2 + x + 1) \mod (x^4 + 1)$: $\Rightarrow (x^4 + 3x^3 + 3x^2 + x + 1) / (x^4 + 1)$ first subtraction: $\Rightarrow (x^4 + 3x^3 + 3x^2 + x + 1) - (x^4 + 1) = 3x^3 + 3x^2 + x$ (final answer)
Given $(3x^5 + x^3 + 1) \mod (x^4 + 1) \Rightarrow (3x^5 + x^3 + 1) / 3x(x^4 + 1)$ first subtraction: $\Rightarrow (3x^5 + x^3 + 1) - (3x^5 + 3x) = x^3 - 3x + 1)$