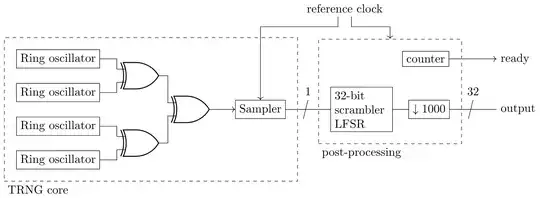
I am using a linear feedback shift register (LFSR) in a scrambler configuration as a randomness extractor for a weakly random source. This source is semi-random (aka. Santha-Vazirani source): the bits are correlated and biased (with a min-entropy of ~0.5 per bit). Here is an example of a LFSR in a scrambler configuration (this one is 12-bit while I am using a 32-bit register) with a downsampler:
The weakly random entropy source feeds the LFSR scrambler directly and the output is highly downsampled (one output bit is taken for every e.g. 1000 weak bits). This method has been proposed here. However, I did not find examples where LFSR scramblers are used as randomness extractors. Hence, I have the following questions:
- Is using a scrambler for randomness extraction of semi-random data a valid use? How does it compare to other extractors? For example, a von Neumann extractor is only suitable for biased, independant (not correlated) input and is linear time.
- How to compute how much downsampling/decimation is required at the output of the LSFR so that the output is suitable for cryptographic use (given an estimation of the input min-entropy)?
- What implications does taking the whole register at once (e.g. output 32 bits every 32000 weak input) rather than 1 bit every 1000 input have?
context: The LFSR is used in the following TRNG: