What are the properties of random involution? What is the difference between random involution and random permutation?
-
8Well, a random involution is an involution chosen at random, while a random permutation is a permutation chosen at random. That's the difference. If you provided a bit more background for your question — like, say, in what context did you come across these things, what do you want to use them for and/or what kinds of properties you're interested in — we might be able to give a more specific answer. – Ilmari Karonen Nov 06 '20 at 02:32
1 Answers
An involution is a function $f$ from a set to itself, such that $f\circ f$ is identity (i.e. applying the function $f$ on the result of the function $f$ gets back to the original element, i.e. $f=f^{-1}\,$). Recall that $\circ$ is function composition.
A permutation is a function $f$ from a set to itself, such that there exists a function $g$ from that set to itself, such that $g\circ f$ is identity (i.e. applying the function $g$ on the result of the function $f$ gets back to the original element). Equivalently, it's a bijection from that set to itself.
It follows that every involution is a permutation. And a permutation $f$ is an involution if and only if $f\circ f$ is identity.
A random involution (resp. permutation) is one chosen (implicitly: uniformly) at random among these over a certain finite set.
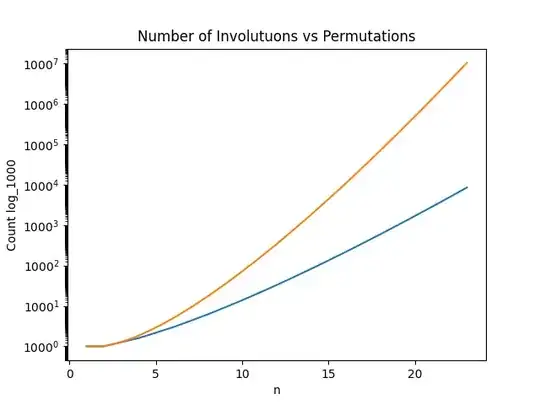
There are $n!$ (OEIS A000142) permutations of a set of $n$ elements, but much less involutions (A000085) for $n>2$. Orange is the number of permutations and blue is the number of involutions.
Among differences of cryptographic significance: a permutation can be one-way, but an involution can't (since any algorithm implementing an involution implements its inverse).
Also: for all $k\in[1,n]$, iterating a random permutation starting from a fixed point cycles on or before $k$ step(s) with probability $k/n$, while for a random involution that's certain when $k\ge2$, and with probability above $1/n$ for $k=1$ and $n>2$.
- 140,762
- 12
- 307
- 587