I know that perturbation should be proportional to the $\text{L}_1$-sensitivity of the function if someone wants ($\epsilon,0$)-differential privacy, and proportional to the $\text{L}_2$-sensitivity of the function if someone wants ($\epsilon, \delta$)-differential privacy for $\delta > 0$.
But why is that? Can anybody describe the intuition behind the use of these two norms? Or maybe share some resources?
I don't think there is a direct between the type of norm and whether $\delta=0$. For example, this crypto.SE answer mentions a mechanism that is pure $\varepsilon$-DP and scales with $L_2$-sensitivity. Conversely, some $(\varepsilon,\delta)$-DP mechanisms scale with $L_1$-sensitivity, like the truncated geometric distribution from this paper.
However, the most commonly used noise mechanisms used in DP are Laplace noise and Gaussian noise, which respectively scale with $L_1$ and $L_2$ sensitivity; the first one is pure $\varepsilon$-DP while the latter only provides $(\varepsilon,\delta)$-DP. You can find a "visual" representation of why that's the case by looking at the density function of a multi-dimensional Gaussian (top) vs. Laplace (bottom):
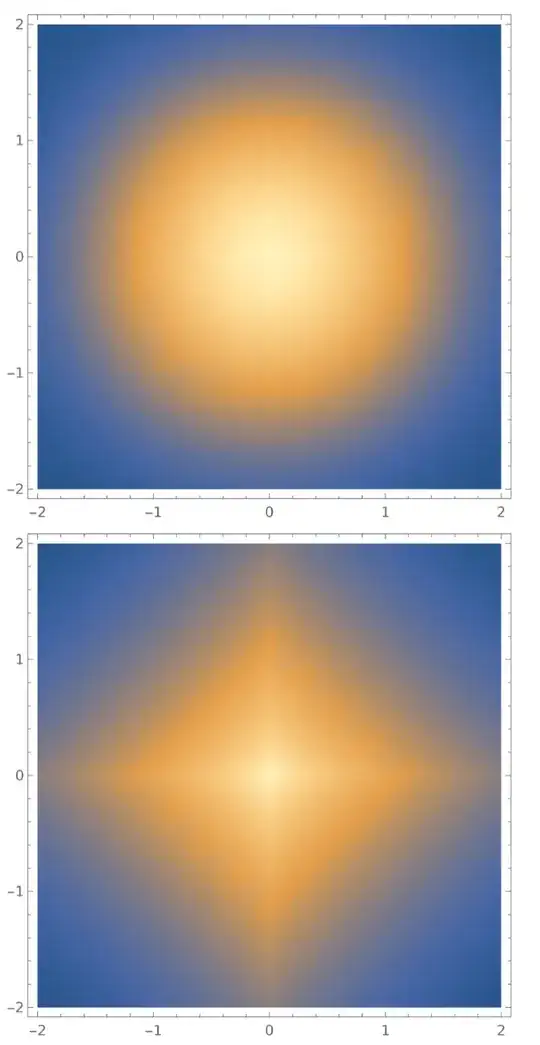
This picture is taken from this blog post of mine about Gaussian noise.
