3

In some text I am reading, there is an exercise asking to show that KeeLoq decryption function is the inverse of the encryption function. Details about KeeLoq are given in the Wikipedia article.

As I am no hardware guy, I have no clue how to approach this problem. Does someone happen to see, how to show the requested property?

e-sushi
  • 17,891
  • 12
  • 83
  • 229
Azooo
  • 225
  • 1
  • 5

1 Answers1

4

It is difficult to find a complete specification, so I'm going by the Wikipedia article you linked.

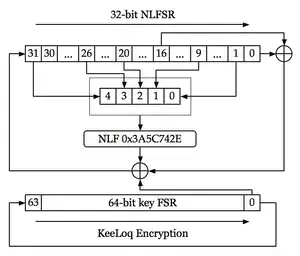
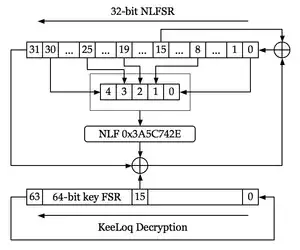
encryption decryption

These images (public domain, from Wikipedia) describe one round of the encryption/decryption algorithm, with 528 rounds in total. At the start, the plaintext is put into the 32-bit shift register, and at the end the ciphertext is taken out of it (for decryption, the other way around).

In each round, actually only one bit of data is actually changed (the new bit with number 31 for encryption, 0 for decryption), the other bits are only shifted around.

If we number all the bits in the "data queue" over time by $L_0 \dots L_{559}$, with bit $j$ before round $i$ being $L_{i+j}$, $L_{i+32}$ is the new bit 31 after round $i$, and we can describe the encryption algorithm as follows (from the text to Figure 1 (page 9) in Periodic ciphers with small blocks and cryptanalysis of KeeLoq, which features a similar image):

  1. Initialize with the plaintext: $L_{31}, \dots, L_0 := P_{31}, \ldots, P_0$.
  2. For $i = 0, \ldots, 528 − 1$ do
    $$L_{i+32} := k_{i\ \bmod\ 64} ⊕ L_i ⊕ L_{i+16} ⊕ NLF(L_{i+31}, L_{i+26}, L_{i+20}, L_{i+9} , L_{i+1})$$
  3. The ciphertext is $C_{31}, \ldots, C_0 := L_{528+31}, \ldots, L_{528} $

The decryption is similar, but here we number the rounds from 528 to 1, and the bits over time as bit $j$ before round $i$ is $L_{i+j}$. $L_{i-1}$ is the output of round $i$.

  1. Initialize with the ciphertext: $L_{528+31}, \dots, L_{528} := P_{31}, \ldots, P_0$.
  2. For $i = 528, \ldots, 1$ do
    $$L_{i-1} := k_{i-1\ \bmod\ 64} ⊕ L_{i+31} ⊕ L_{i+15} ⊕ NLF(L_{i+30}, L_{i+25}, L_{i+19}, L_{i+8} , L_{i+0})$$
  3. The plaintext is $P_{31}, \ldots, P_0 := L_{31}, \ldots, L_{0} $

Now all that stays to show is that both equations $$L_{i-1} = k_{i-1\ \bmod\ 64} ⊕ L_{i+31} ⊕ L_{i+15} ⊕ NLF(L_{i+30}, L_{i+25}, L_{i+19}, L_{i+8} , L_{i+0})$$ and $$L_{i+32} = k_{i\ \bmod\ 64} ⊕ L_i ⊕ L_{i+16} ⊕ NLF(L_{i+31}, L_{i+26}, L_{i+20}, L_{i+9} , L_{i+1})$$ are indeed equivalent. (This is a simple index-shift, and reordering some terms.)

Paŭlo Ebermann
  • 22,656
  • 7
  • 79
  • 117