Overview of relations between cryptographic primitives?

Question

Is there a web page that gives a graphical (or, alternatively, a textual) overview of known implications and separations between cryptographic primitives?

More specifically, I am looking for something like the following, but more comprehensive and with references to the respective works. (The following graphic is taken from a set of slides by Danny Harnik and Moni Naor that I found on the Internet.)

Update (Jan 24, 2023)

Created an interactive visualization of the relationships between cryptographic primitives and open-sourced it at https://github.com/matthiasgeihs/crypto-graph. Contributions are welcome!

Does https://crypto.stackexchange.com/questions/39735/whats-a-cryptographic-primitive-really/52058#52058 help any... — Paul Uszak, Oct 17 '17 at 20:29

score 17 · Accepted Answer · edited Nov 05 '22 at 16:41

17

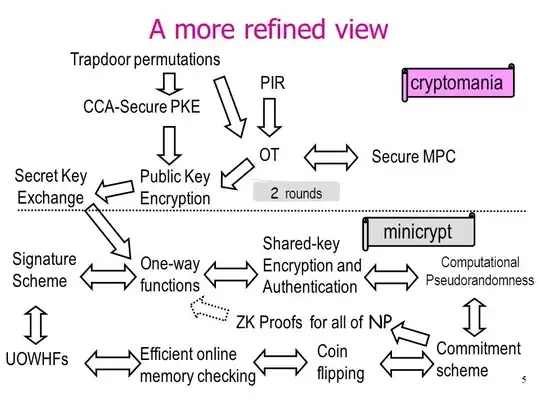
You'll find it in any textbook on basics of cryptography, for example Foundations of Cryptography by Goldreich. I have added a figure which sums up the relationship between the primitives: arrow represent reductions (i.e. $A\rightarrow B$ means that primitive $B$ can be constructed in a black-box manner from primitive $A$) and dashed arrows represent separations (i.e. $A$--$> B$ means that primitive $B$ cannot be constructed in a black-box manner from primitive $A$). The asterisk denotes folklore results (but feel free to correct me if it is wrong).

(1. I'll add other primitives (FHE, iO...) and assumptions (Factoring, DLP...) in due course.

Please correct any mistakes in implications/separations or references.)

Note that this is a screenshot from an active page Relations in Cryptography produced by mti

Abbreviations

C: Commitments
CFP: claw-free permutation
CRHF: collision-resistant hash function
DLP: discrete-logarithm problem
DS: digital signature
OWF: one-way function
OWP: one-way permutation
TDP: trapdoor permutation
OT: oblivious transfer
MPC: multi-party computation
PKE: public-key encryption
PRG: pseudo-random generator
PRF: pseudo-random function
PRP: pseudo-random permutation
SKE: symmetric-key encryption
UOWHF: universal one-way hash function
ZKP: zero-knowledge proofs for NP

References.

[D]: Damgård. Collision Free Hash Functions and Public Key Signature. Eurocrypt’87.

[GGM] Goldreich, Goldwasser and Micali. How to Construct Random Functions. JACM’86.

[BM] Blum and Micali. How to Generate Cryptographically Strong Sequence of Pseudorandom Bits. SIAM JoC’82.

[EGL] Even, Goldreich and Lempel. A Randomized Protocol for Signing Contracts. CACM’85.

[GMR]: Goldwasser, Micali and Rivest. A Digital Signature Scheme Secure Against Adaptive Chosen-Message Attacks. SIAM JoC’88.

[GMW1]: Goldreich, Micali and Wigderson. How to Play any Mental Game: A Completeness Theorem for Protocols with Honest Majority. STOC’87

[GMW2]: Goldreich, Micali and Wigderson. Proofs that Yield Nothing but their Validity or All Languages in NP Have Zero Knowledge Proof. FOCS’86

[H+]: Håstad, Impagliazzo, Levin and Luby. A Pseudorandom Generator from Any One-Way Function. SIAM JoC’99.

[IR] Impagliazzo and Rudich. Limits on the Provable Consequences of One-Way Permutations. STOC’89.

[LR] Luby and Rackoff. How to Construct Pseudorandom Permutations from Pseudorandom Functions. SIAM JoC’88.

[N] Naor. Bit Commitment using Pseudorandom Generator. JoC’91.

[NY] Naor and Yung. Universal One Way Hash Functions and their Cryptographic Application. STOC’89.

[Rom] Rompel. One way Functions are Necessary and Sufficient for Secure Signatures. STOC’90.

[Rud] Rudich. PhD Thesis

[S] Simon. Finding collisions on a one-way street: Can secure hash functions be based on general assumptions? Eurocrypt’98

[Y] Yao. Theory and Applications of Trapdoor Functions . FOCS’82

This was the original image of the answer.

edited Nov 05 '22 at 16:41

kelalaka

48,443
11
116
196

answered Oct 17 '17 at 20:58

ckamath

5,188
2
21
41

Q: Is it possible to use TikZ code here? – ckamath Oct 17 '17 at 21:04
1

@biv should be able to help you with that I think – Ella Rose Oct 17 '17 at 21:56
1

EGL actually requires an enhanced trapdoor permutation; see Appendix in the second volume of Goldreich's FoC. – fkraiem Oct 18 '17 at 00:27
Also this. – fkraiem Oct 18 '17 at 00:35
1

I think it would be worth for the community to create a webpage summarizing these relations. Somewhat like the "complexity zoo" webpage. I am thinking about creating such a page. What do you think? Would that be helpful? – mti Oct 18 '17 at 12:57
I would love to see something similar that covers oracles in terms of the underlying assumption (strong v. weak). – floor cat Oct 19 '17 at 03:58
@mti: It would most certainly be helpful! – ckamath Oct 19 '17 at 07:09
@floorcat: That too would be a good exercise. – ckamath Oct 19 '17 at 07:10
1

@Occams_Trimmer I have been setting up a website for this: Relations in Cryptography. You may want to add it to your answer as a reference. Please also feel free to comment on it. I want to further extend it. – mti Oct 23 '17 at 14:59
@mti: The website is really cool. :) One suggestion: you should add Wikipedia links to the nodes. – ckamath Oct 23 '17 at 15:10
@mti The existence of target collision resistance hash function is equivalent to the existence of one-way functions. – Blanco Feb 20 '19 at 14:27
Why is not there an arrow: PRP $\rightarrow$ PRF? – Blanco Feb 24 '19 at 14:59
It could be added, but is trivial in some sense (the same way OWPs imply OWFs). – ckamath Feb 27 '19 at 15:40
1

Removed the link to the website. I just don't have enough time at the moment to fix the 'due course' bit. Will try it soon. :) – ckamath Sep 03 '19 at 08:34
There are a lot of really important arrows missing. For example the one from CRHF to C or the one from TDP to OWP. – UTF-8 Feb 01 '20 at 13:15
Is there something similar for capabilities? Like authentication, secure communication, safe remote computing, etc? – Stephane Bersier Nov 28 '20 at 21:52
1

@ckamath Updated link to website: Relations in Cryptography – mti May 28 '22 at 13:57
it would be great to have Abbreviations table like the one in this post in the website as well – baro77 Sep 30 '22 at 07:06
@mti thanks for the website. – kelalaka Nov 05 '22 at 16:44
1

@kelalaka Upon request via twitter, open-sourced the page at https://github.com/matthiasgeihs/crypto-graph. Contributions are welcome :) – mti Jan 24 '23 at 11:36

Overview of relations between cryptographic primitives?

Update (Jan 24, 2023)

1 Answers1

Linked