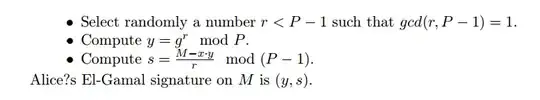How to find $r$ for El-Gamal signature with known private key

Question

For public key $(g,b,P)$ and private key $x$ I have that...

x = 8437809068483222013573558289468531414326215630180218801941732905
P = 7339893940555892950021117953932742794751344995120378281984000000000001
g = 89
b = 4912876245630500045238873065831524614701581692824065606616840403034906

I am trying to find the random number r used in signing

M = 178197212211208201211210146110

where the (y,s) are

y = 4888362675268704701803932900979085359299230032137217762234865463825395
s = 2972754454246783222682468852246694620839545754907463463768712881658815

I am using the signature scheme here and I thought I could solve for $r=\frac{M-xy}{s} \mod (P-1)$ but I keep getting

r=6586066995309612052451381515420731372587693346972879972770753040391021

but then $y=g^r \mod P$ isn't true.

---

The instructions indicate:

Answer 1

$r\cdot s\bmod (P-1) = 6586066995309612052451381515420731372587693346972879972770753040391021\cdot 2972754454246783222682468852246694620839545754907463463768712881658815 \bmod 7339893940555892950021117953932742794751344995120378281984000000000000$

yields

720487199053255869302957380434219754352470619914582568375746711500115,

whereas

$M-x\cdot y\bmod (P-1) = 178197212211208201211210146110-8437809068483222013573558289468531414326215630180218801941732905\cdot 4888362675268704701803932900979085359299230032137217762234865463825395 \bmod 7339893940555892950021117953932742794751344995120378281984000000000000$

yields

4218349912365743958467337126869664026873136130922995548817354564023635.

Are you sure that you invert $s$ modulo $(P-1)$ correctly?

PS: No need to ask a new question for the same problem if you don't get an answer within 6 hours. Most regular users don't look just at the front page. After few days you can then change the text a little bit (like the others do) to get your question to the front page again.

Answer 2

You have to observe that with the given values, $s$ is not co-prime to $P-1$. Hence, you cannot directly compute $r$ as $(M-xy)/s \bmod (P-1)$.

We have $\gcd(s,P-1) = 185$. Let $q_1 = (P-1)/185$. Then $$r \bmod q_1 = (M-xy)/s \bmod q_1 = 3956222280490813791400244134782922347290756609897677447028095051944$$

It remains to compute $r \bmod 185$. Note that $185 = 5 \times 37$. There is a slight complication because $\gcd(q_1,185) = 5$. Define $q_2 = 37$ and $q_3= 5$. Note that $P-1 = q_1 \times q_2 \times q_3$.

From $y = g^r \bmod P$, we get $y^{(P-1)/37} \equiv {g^{((P-1)/37)}}^{r \bmod 37} \pmod P$. By brute force, we find $r \bmod 37= 5$.

Chinese remaindering only allows one to obtain $r \bmod q_1 q_2$ (since $\gcd(q_1,q_3) \neq 1$). We get $$r \equiv 718108065145388506225887396409320059133908107486475023802228095051944\pmod {q_1q_2}$$

---

EDIT: Please check the correctness of your exercise. Also note that $P-1$ is smooth: $$P-1 = 2^{49} \times 3^{23} \times 5^{12} \times 7^9 \times 11^4 \times 13^5 \times 17^3 \times 19^2 \times 23^3 \times 29 \times 31 \times 37 \times 41 \times 43 \times 47$$ You can therefore make use of Poligh-Hellman algorithm to compute $r$ from $y = g^r \bmod P$.