How to attack polyalphabetic affine cipher with only ciphertext?

Question

How to attack polyalphabetic affine cipher with only the ciphertext?

A polyalphabetic affine cipher can be seen as the composition of an affine cipher ($p \mapsto c \equiv a \times p + b \pmod{26})$ and a Vigenère cipher.

Consider we have a key such as $(a_{n\ mod\ 3},b_{n\ mod\ 3}) \in [(3,1); (7,2); (11,8)]$.
For instance itwas$_{plaintext}$ $\longrightarrow$ zgpbd$_{ciphertext}$.

Answer 1

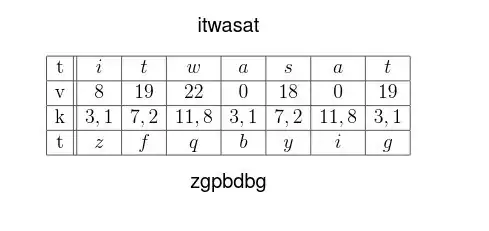
This is a simple variant of the Vigenère cipher, and can be broken in basically the same way:

First, you need to determine the key length. The standard methods for doing this for any Vigenère-like cipher, like Kasiski examination or calculating the index of coincidence, work just fine here.

Once you've determined that the key most likely consists of $k$ separate affine maps, you then split the plaintext into $k$ columns, each encrypted with a different affine map, and break each of them like you'd break a normal monoalphabetic affine cipher, using letter frequency analysis.

---

Note that crib dragging or $n$-gram frequency analysis generally won't work for solving the columns, since the letters in each column aren't consecutive in the plaintext. On the other hand, since you have multiple columns taken from the same plaintext, you can mostly solve the cipher without knowing the actual letter frequency distribution of the plaintext (as long as it's sufficiently non-uniform).

To do that, simply take the letter frequencies from one of the ciphertext columns (say, the first one) and use them instead of the expected plaintext letter frequencies to solve all the other columns. Assuming that you have enough ciphertext for the statistical analysis to yield robust results, and that the plaintext doesn't just happen to contain any repetitive elements with period equal to the key length, this should give you a "pseudo-key" that, when used to decrypt all the other columns, will convert them to the same cipher alphabet as the first one. Thus you can effectively reduce the polyalphabetic cipher into a monoalphabetic one, which you can then solve e.g. by brute force.

(For increased robusteness, you can do the same thing with each of the ciphertext columns as the reference column, and check that the resulting affine maps between the columns are consistent with each other. If you find any mismatches between the maps suggested as most likely by frequency analysis, that can be a sign that some columns don't have sufficiently similar plaintext letter frequency distributions. In that case, you may want to examine the other reasonably likely maps found by frequency analysis to see if they'll solve the mismatch.)

This works because affine maps form a group. In particular, the inverse of any affine map is an affine map, and so is the composition of any two affine maps. Thus, decrypting a ciphertext column with one affine key and re-encrypting it with another is always equivalent to encrypting (or decrypting) it with some third key. The same trick works for ordinary Vigenère ciphers too, and for any other repeating-key substitution cipher (like the XOR cipher) whose underlying monoalphabetic substitutions form a group.