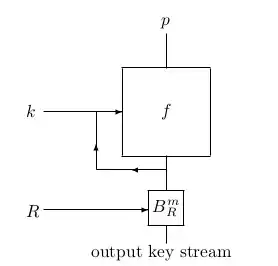
The output of the block cipher is used as the new key, and also passed to the "output block" function, which is referenced in the NIST document as $B^m_R$.
The purpose of the IV $R$ and the function $B^m_R$ is to reduce the output to a smaller size in a manner that hides the true output of $f$. Too large an output allows key recovery.
The output of this function is an $m$-bit value, which is then used to build the keystream. The inputs are $R$ and the $n$-bit output of the block cipher. $R$ is a binary $m \times n$ matrix, and is multiplied against the block cipher output modulo 2 arranged as an $n \times 1$ matrix, resulting in a matrix of $m \times 1$ bits, which is used for the output.
An example of this uses the following:
$f = $ AES-128
$n = 128$
$m = 8$
$R$ would be an $8 \times 128$ matrix and require 128 bytes to build, and when multiplied against the 128-bit output of AES, would result in 8 bits of data (1 byte) for the keystream. $R$ must be unique to each message, and must be random and non-zero, but does not need to be secret. It can be built using a smaller amount of bits using appropriate methods (such as HKDF), as long as at least $n$ bits are used to generate it.
The constant input $p$ does not have any special requirement and is generally some constant, possibly even all 0 bits.
It is obvious that with a small output and the need to perform the key schedule for every iteration, the efficiency of KFB is very low, and thus it is generally not used for practical applications, despite the provable security bounds.
I assume a partial key feedback mode could be made using AES-256 with 128 of the key bits fixed, and the rest fed back from the output, or using some kind of shift mechanism.