I am trying to understand the small subgroup confinement attack on the Diffie-Hellman algorithm. I will present the attack and try to explain why it works.
Small subgroup confinement attack on the Diffie-Hellman algorithm
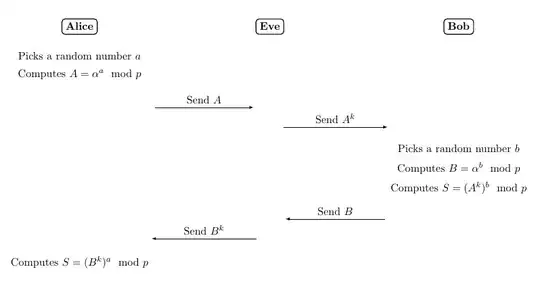
Let $\mathbb{Z}_p^*$ be a group, where $p$ is a large prime and let $\alpha$ be a primitive root modulo $p$. Let's consider that Alice and Bob want to do a key agreement on the whole cyclic group $\mathbb{Z}^*_p$ using the Diffie-Hellman algorithm. The following sequence diagram illustrates how Eve can perform a small subgroup confinement attack:
By doing this, if $k$ is well-chosen, the secret $S$ can be found by exhaustive search.
How to choose the $k$-value
As $p$ is a prime number, the order of $\mathbb{Z}^*_p$ is a composite, so there exist subgroups. Say $\mathbb{G}_w$ is one small subgroup of prime order $w$. So by picking $k = \frac{p-1}{w}$, the secret value $S \in \mathbb{G}_w$ can be found by exhaustive search, efficiently, in the small subgroup $\mathbb{G}_w$.
Why does it work?
In this section I will try to prove that $S \in \mathbb{G}_w$.
We know that $w\text{ | } (p-1)$, so $\exists k$ such that $p-1 = w \times k$. Plus, we know that $\mathsf{ord}(\alpha) = p - 1$ because $\alpha$ is a primitive root modulo $p$ and a consequence of Cauchy's theorem is that, given an element $x$, $\mathsf{ord}(x^k) = \frac{\mathsf{ord}(x)}{(\mathsf{ord}(x) \wedge k)}$. (Here, $\wedge$ denotes the greatest common divisor between two numbers.) So, in our case, we have:
$$\mathsf{ord}(\alpha^{ab(p-1)/w}) = \mathsf{ord}(\alpha^{abk}) = \frac{\mathsf{ord}(\alpha)}{(\mathsf{ord}(\alpha) \wedge abk)} = \frac{(p-1)}{((p-1) \wedge abk)} = \frac{wk}{ (wk \wedge abk)}$$
And, we know that $(wk \wedge abk) = k$, because $w$ is a prime number. Therefore,
$$\mathsf{ord}(\alpha^{ab(p-1)/w}) = \frac{wk}{k} = w$$
As a result, we can conclude that $S \in \mathbb{G}_w$.
Could someone approve or disapprove my demo?