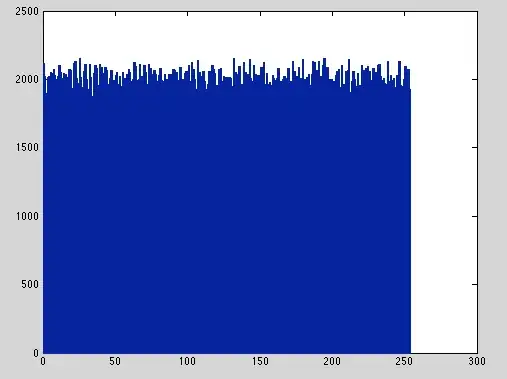
I am not exactly sure if this is for math stackexchange or crypto:
A TRNG outputs numbers in $[0,1]$ in a Gaussian distribution. I would like to convert them into uniform random bytes ($[0,255] $) to perform byte operations. What is s cryptographically secure method of doing this?
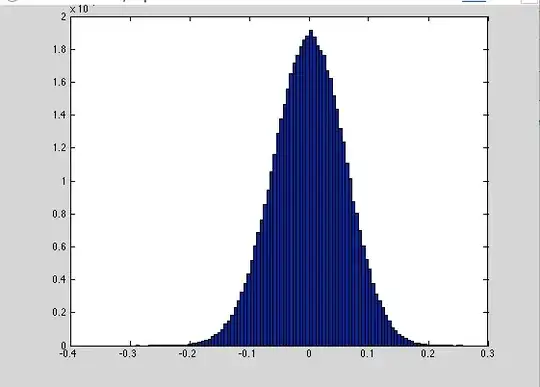
Here is an example distribution from my generator before normalized between $[0,1]$:
Edit:
Output from my original methodology: Normalize values to to be within $[0,1]$, remove first and second decimal place via $x*100-floor(x*100)$, then put between value discrete values in $[0,255]$ via $floor(x*255)$. The resulting distribution is as follows: