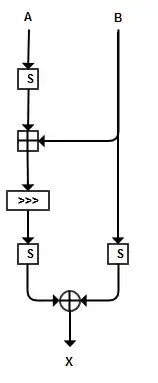
From your picture I deduce that $A$ and $B$ are both 8 bits.
So this construction can be seen as a $16 \times 8$ bit S-box (not bijective). The fact that it's not square is probably what is causing confusion.
Usually, for SPNs, invertible S-boxes are used. Non-invertible S-boxes are less common, but they certainly have applications.
One of the things we can do to determine the weakness of an S-box with respect to differential cryptanalysis, is to look at the difference distribution table (DDT).
That's just a table where each row (column) represents an input (output) difference. The entries are equal to the amount of times the output difference occurs for the input difference. If a certain input difference $\Delta X$ often leads to output difference $\Delta Y$, then this is considered a weakness.
So, how is the value you compute related to the DDT?
My testing algorithm is essentially to loop through all A and B values
for all potential input differentials (ΔA or ΔB), and count how many
distinct output differentials are seen for each input differential.
For a given input difference $(\Delta A, \Delta B)$ (this corresponds to a row), you compute the amount of columns (output differences) that have a nonzero DDT entry on that row.
For S-boxes that are not square, this doesn't really tell us a lot about the strength with respect to differential cryptanalysis. For square S-boxes, it may be some kind of average indicator (which is probably not very useful).
It does explain why you get 255 though. The amount of columns in the DDT equals $2^8 = 256$. The output difference $\Delta Y=0$ only occurs when $\Delta X = 0$. I assume you didn't count those (the result would be 1). This means that there are at most $256 - 1 = 255$ nonzero entries in a row.
For common $8 \times 8$ S-boxes that would indeed be theoretically optimal (unfortunately that's not possible, even in theory).
But in your case, given that there are $2^{16} = 65536$ (256 times as many) input values, you can indeed get 255 nonzero entries.
(Sorry if the above was not entirely correct, I may have misunderstood the way you compute the "score".)
I computed the DDT for this structure, scaled to an $8 \times 4$ system. With $S$ a very good $4 \times 4$ S-box, the result isn't a very good S-box. Of course it's dangerous to extrapolate to a larger size, but I see no reason why this structure would be particularly good.