GCM and CBC modes internally work quite differently; they both involve a block cipher and an exclusive-or, but they use them in different ways.
In CBC mode, you encrypt a block of data by taking the current plaintext block and exclusive-oring that wth the previous ciphertext block (or IV), and then sending the result of that through the block cipher; the output of the block cipher is the ciphertext block.
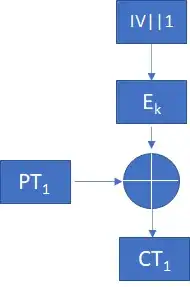
GCM mode provides both privacy (encryption) and integrity. To provide encryption, GCM maintains a counter; for each block of data, it sends the current value of the counter through the block cipher. Then, it takes the output of the block cipher, and exclusive or's that with the plaintext to form the ciphertext.
Note two key differences:
What's being exclusive-or'ed; in CBC mode, the plaintext is exclusive-or'ed with data that the attacker knows (the IV or a previous ciphertext block); hence, that in itself does not provide any inherent security (instead, we do it to minimize the chance that we send the same block twice through the block cipher). In GCM mode, the plaintext is exclusive-or'ed with output from the block cipher; it is inherent in the security model that the attacker cannot guess that output (unless he already knows the plaintext and the ciphertext).
What's being sent through the block cipher; in CBC mode, the plaintext is sent through the block cipher (after it's been 'randomized' with an exclusive-or); in GCM mode, what's being sent through the block cipher doesn't actually depend on the data being encrypted, but instead only on internal state.
As for how GCM uses an IV (I personally consider 'nonce' a better term for what GCM uses, because that emphesizes the idea that with GCM, you cannot use the same nonce for the same key twice), well, it is used to initialize the counter.