Parallel hash construction

Question

I'm wondering why hash constructions aren't parallel like CTR mode for encryption?

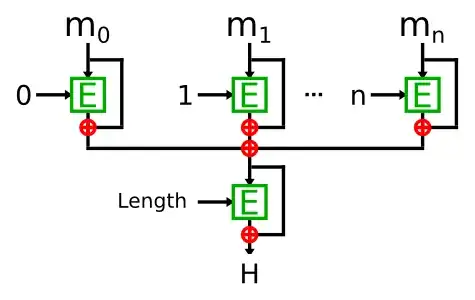
For example: We have ideal block cipher E, where we encrypt message block with counter and xor output block with message block. Then we xor (sum) all blocks and encrypt it with length of message and xor with sum of all blocks to get hash. If last message block is shorter than block size it is padded with zeroes.

$H_{0} = E_{0}(m_{0}) \oplus m_{0}$

$H_{1} = E_{1}(m_{1}) \oplus m_{1}$

$...$

$H_{n} = E_{n}(m_{n}) \oplus m_{n}$

$H_{sum} = H_{0} \oplus H_{1} \oplus ...\oplus H_{n}$

$H = E_{Length}(H_{sum}) \oplus H_{sum}$

Parallel hash construction example

Is such construction known to be insecure? Or is it secure?

You can build a hash the same way you build a MAC. If you look at how PMAC works you'll see why your construction is wrong and how to fix it — user1028028, Jun 02 '14 at 07:51
@user1028028: PMAC without key is completely insecure. Fix it, how? — LightBit, Jun 02 '14 at 16:18

score 7 · Answer 1 · answered Jun 01 '14 at 02:23

7

Dmitry said that a collision in the xor can be found with a generalized birthday attack.

Actually, it's a lot worse than that; second preimages of sufficiently long messages can be found in polynomial time; hence an enormous block size (which might help against the birthday attack) doesn't help.

Let us call the size of the output of the ideal block cipher $n$. Then, let us consider a message that consists of (at least) $n$ blocks; and for each block, we consider two distinct alternatives, at position $i$, we would have arbitrary selected blocks $M_i$ and $M'_i$.

We would then compute $H_i = E_i( M_i ) \oplus M_i$ and $H'_i = E_i( M'_i ) \oplus M'_i$.

If we have a target value $Z$ for the exclusive or's (which we would have for a second preimage problem), we would then consider what sum of $H_i$ and $H'_i$ would exclusive-or to the target values; this can be viewed as a linear algebra problem, and can be solved with, say, Gaussian elimination in time $O(n^3)$

answered Jun 01 '14 at 02:23

poncho

147,019
11
229
360

If $E$ were replaced with another hash function and still incorporated the length and the index, then would it be secure? – Melab Oct 20 '23 at 21:35
@Melab: no; it wouldn't frustrate the attack at all - the attack doesn't assume invertibility of $E$, so replacing it with a noninvertible function doesn't help. – poncho Oct 26 '23 at 14:30
Does this mean there is no secure parallelizable hash that is based on the XOR sum of data blocks individually processed along with their indices using a known secure hash algorithm? – Melab Nov 15 '23 at 03:34
What if the final hash operation on the XOR sum used a different function? – Melab Dec 04 '23 at 13:52
@Melab: that would depend entirely about what that different function is - if it is a strong hash function, than it is easy to show that the construction is secure. – poncho Dec 04 '23 at 14:00

Dmitry Khovratovich · Accepted Answer · 2014-05-31T22:41:13.653

4

It is insecure, since the XOR of many ($n$) independent compression function is much more vulnerable to collision attacks. The generalized birthday attack finds a collision with complexity $$ 2^{\frac{\text{block size}}{1+\lg n}}. $$

edited May 31 '14 at 22:41

answered May 31 '14 at 11:24

Dmitry Khovratovich

5,647
21
24

So XOR MACs are only good up to $2^{\frac{n}{2}}$ blocks? – Melab Dec 06 '17 at 23:25

Parallel hash construction

2 Answers2

Linked