I was unable to solve the multiplication table given in the book for $\mathrm{GF}(2^2)$.However, I have managed to solve the addition table.
Acoording to the Book multiplication is the AND operation, but when I applied this I did not get the answer given in the book.
This is the Table given in the book:
I couldn't replicate the same answers for 10x10 or 11x11.
$\mathrm{GF}(2^2)$ is the finite field of 4 elements, and has minimal polynomial $x^2+x+1$. Throughout this question I will use $ab$ to denote $ax+b$ (ie $10=1*x+0$) - this is standard notation when considering finite fields over $\mathbb F_2$ since it aligns with how we consider bits in bytes.
As you have already seen, addition is done by bitwise xor:
$ab+cd := ab\oplus cd$
For multiplication, we do standard polynomial multiplication, but then must reduce by the minimal polynomial. That is, we use the identity that $x^2=x+1$. So:
$$\begin{aligned} ab\cdot cd &= (a*x+b)(c*x+d) \\ &= (a * c)x^2+(a* d + b * c)x + b*d \\ &= (a* d + b * c + a * c) x + [b*d + a * c] \end{aligned}$$ Now, as discussed above + is xor (denoted $\oplus$), and the hint given by your book is that multiplication of the coefficients is the same as an AND operation (which I'll denote with $\&$):
$$\begin{aligned} ab\cdot cd &= (a\&d \oplus b\&c \oplus a\&c) x \oplus [b\&d \oplus a\&c] \\ &= [a\&d \oplus b\&c \oplus a\&c][b\&d \oplus a\&c] \end{aligned}$$
There are a number of ways to represent elements of the field; we'll start by representing them as polynomials with degree at most 1, and with integer coefficients modulo 2. There are four such polynomials: {0, 1, x, x + 1}.
Here are the addition and multiplication tables:
+ 0 1 x x + 1
0 0 1 x x + 1
1 1 0 x + 1 x
x x x + 1 0 1
x + 1 x + 1 x 1 0
⋅ 0 1 x x + 1
0 0 0 0 0
1 0 1 x x + 1
x 0 x x2 mod m x2 + x mod m
x + 1 0 x + 1 x2 + x mod m x2 + 1 mod m
Hold on. What's that funny-looking m?
It's a "reduction polynomial" which brings the product back down to degree 1 or less. It has to be a polynomial of degree 2. There are four such polynomials: let's try each and see what we get.
x2
0 x
x 1
x2 + 1
1 x + 1
x + 1 0
x2 + x
x 0
0 x + 1
x2 + x + 1
x + 1 1
1 x
Note that the first three polynomials all factor into products of lower-degree polynomials: x2 = x(x), x2 + 1 = (x + 1)(x + 1), x2 + x = x(x + 1). Only x2 + x + 1 is prime; and this prime reduction polynomial generates a complete multiplication table with no 0s. This is a necessary condition to be a field. Our final tables are:
+ 0 1 x x + 1
0 0 1 x x + 1
1 1 0 x + 1 x
x x x + 1 0 1
x + 1 x + 1 x 1 0
⋅ 0 1 x x + 1
0 0 0 0 0
1 0 1 x x + 1
x 0 x x + 1 1
x + 1 0 x + 1 1 x
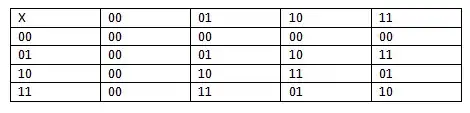
We can also write our elements in binary form: 0 => 00, 1 => 01, x => 10, and x + 1 => 11. In this notation our tables become:
+ 00 01 10 11
00 00 01 10 11
01 01 00 11 10
10 10 11 00 01
11 11 10 01 00
⋅ 00 01 10 11
00 00 00 00 00
01 00 01 10 11
10 00 10 11 01
11 00 11 01 10
01=1; 10= 2; 11=3 ; 01* 10= 1*2=2= 10 Just convert the two bits into decimal and apply multiplication. The result of multiplication should be converted into binary again and hence , inserted within the table.
