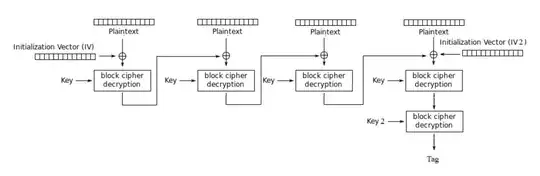
The question is about a MAC built from a block cipher, which we assume has a fixed-size block, and XOR of blocks. This implies that any IV(s) are the same size as a block, as in the drawing. Thus we must ignore everything about variable or random-size IV that popped in the question between it's revisions 4 and 5.
In a Message Authentication Code scheme, the same algorithm is used by sender to compute a bitstring called the MAC (or tag) from message and key, and by the verifier to recompute a MAC from received message and key (with the recomputed MAC compared to the received MAC to decide if the received message is accepted or not). Adversaries knowing everything of the method except Key(s), thus including IVs, and allowed to get examples of (Message, MAC) pairs possibly including for messages of their choice, are trying to make a (Message', MAC') pair with new Message' that passes verification, with probability sizably better than supplying a random MAC. Unless otherwise stated, messages are assumed to be variable size (though in the drawing, that size much be a multiple of the block size).
If either of IV and IV2 in the question's drawing are changed randomly at each message (as considered in some of the variants of the questions and comments), then the IV(s) that can change must be transmitted along the value labeled "Tag" in the drawing, or made part of the MAC (at the expense of not having quite the same algorithm for the verifier). Argument: without both IVs, the verifier would be unable to recompute the right "Tag". Therefore, we have to assume that adversaries, which already are assumed to be able to change the message and the MAC, are able to change the variable IV(s) too.
It's easy to show that in this case, a simple attack breaks the security of the MAC. The links in the question are about that. Specifically: with a random IV part of the MAC, given a single example of (Message, MAC) pair, it's possible to make another (Message', MAC') pair that passes verification, with Message ≠ Message'. When that attack is identified, it's easy to see that the addition of random IV2 (if part of the MAC) only worsen things.
Thus it's essential for security that both IV(s) in the drawing are fixed (or equivalently, transmitted by some channel secure against alteration; or determined from the message; but nothing in the question suggests either, so I won't consider these non-standard hypothesis any more). Further, the standard definition of a MAC scheme is with any IV that it might use fixed and public.
Assuming fixed and public IVs from now, here are a few things that can be shown:
- With removal of the block with Key 2 (or if Key 2 equals Key 1), and variable message size, there's a computationally easy attack on the MAC. The addition of an independent Key 2 (as in the drawing), or replacing the last block using Key 1 by one with Key 2 different from Key 1, or fixing the message size, or including the message size in the first message block, are four common methods to prevent that easy attack.
- In the drawing's configuration, there's a Meet-in-the-Middle attack recovering the $k$-bit MAC key formed by Key 1 ∥ Key 2 (each $k/2$-bit), with cost $\mathcal O(2^{k/2})$ block cipher evaluations and a lot of memory (with some time vs memory tradeoffs possible). A common method to prevent that attack for most practical purposes is the addition of an additional block with Key 1 after the one with Key 2, as in Retail MAC (aka Enhanced Security DES MAC, rMAC, ISO/IEC 9797-1 MAC Algorithm 3).
- There's another attack requiring $\mathcal O(2^{b/2})$ queries to a device computing and disclosing the MAC given a message, where $b$ is the bit width of the block cipher; and $\mathcal O(2^{k/2})$ block cipher computations to recover Key 1 then Key 2. That attack can in practice be more efficient than MitM, if only because it uses much less memory. Also it works including with the aforementioned countermeasure against MitM. To prevent that attack we want to make it impossible that adversaries get any near $2^{b/2}$ MACs, by choosing a block cipher with large block size, or (including and) a block cipher with a large key (AES-128 leads to $b=128$ and $k=256$, which is fine in both regards for most applications); or, as a fallback, counting and limiting the MACs generated, or slowing MAC generation to the same effect.
For all attacks in that second part of the answer, the addition of one or two fixed public IVs chosen randomly does not help. I suggest to show that any attack that works against the scheme without IVs can be adapted to work against the scheme with IVs. That holds for IV and IV2 independently.
Combined with the fact that it's the IVs that allow attack in the first part, that's probably why the many variants of CBC-MAC generally do without IV at all, or use an all-zero IV.