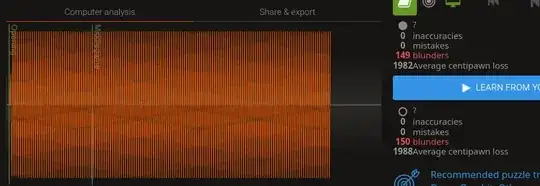
Since mate is evaluated as a finite centipawn loss, all games have a finite average centipawn loss. I stumbled upon this Reddit r/chess thread where this game has an average centipawn loss of 1971 vs. 1981, but maybe it's possible to achieve a greater average centipawn loss.
Question: What's the theoretical worst average centipawn loss on LiChess?
Here I'm not interested in chess variants.
I imported this game (adapted from the above) which gives an average centipawn loss of 1982 vs. 1988; here LiChess evaluated to move 150 (unlike the above game, where LiChess only evaluated to move 100 (although it's still slightly better (1972 vs. 1982) when evaluated to 100 moves, since the queen is hanging on the 3rd ply)).