I'm so confused about this. I googled it and read about knight's tours, however they all start from illegitimate positions. I want to know if a knight can move through all squares from its original position (e.g. b8, g8, b1, and g1).
Asked
Active
Viewed 8,795 times
27
1 Answers
58
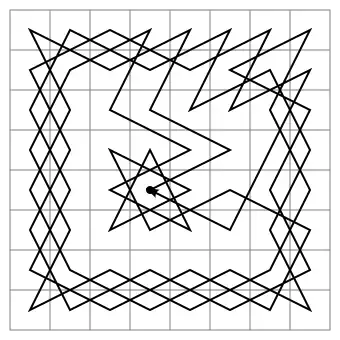
Yes, it can
This particular knight's tour is closed, meaning that it starts and finishes in the same square. Therefore, the knight can start at any square on the board and finish on the same square, since it just starts at a different point along the cycle.
Aric
- 2,081
- 1
- 19
- 41
-
6
-
5Except, what kind of sorcery is used from f3 to h7... a double-jump?! EDIT: Ah, it is actually a double jump. – PascalVKooten Aug 20 '18 at 15:42
-
I suppose you can also make an open knight's tour (i.e. not a cycle) that starts from b1 and terminates at g1? – Jeppe Stig Nielsen Aug 20 '18 at 20:48
-
move through all squares from its original positionalso meanswithout visiting the same square twice(which I don't). So it's just two interpretations of the requirements. That's fine. – ispiro Aug 20 '18 at 19:38