2

To find the degree (or the number of attacked squares), of a square's corresponding vertex for all pieces and their corresponding graphs, given any square of the board. In other words, given a piece and a square - the number of attacked squares by the piece at the given square on an empty board is what the student finds. This is repeated until all squares are examined.

Also, has anyone had the idea to make a 3-D representation for each piece, where each square has a respective height equal to the degree of its' corresponding vertex in the given piece's graph (where the degree is the number of squares attacked by each specific piece at each square)? Of course, the rook's graph representation would be dull, as the graph is regular (ie the number of attacked squares is the same at any square), but all the other pieces, save for the pawn, would give students the visual lesson that the pieces in the center have more options. Not only this, it appeals to an old military adage - to control the high ground - which in these cases is the center, if at all possible.

TuringTux
  • 197
  • 1
  • 12
Paul Burchett
  • 595
  • 3
  • 11
  • Why the votes to close? I asked a question about the game, and the way it's taught. Now, whether the exercise is effective or not, that's a whole other question.

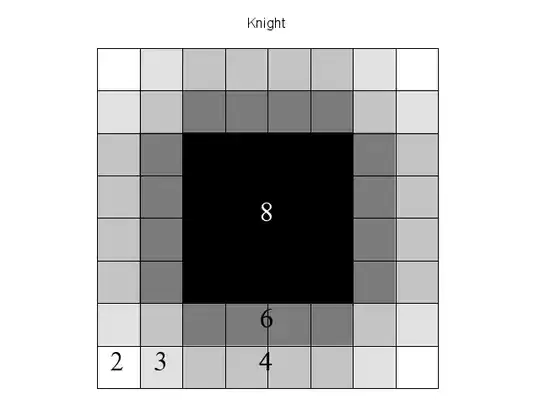
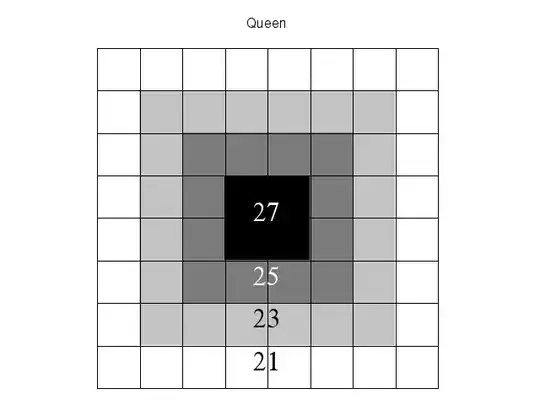
    Just so you know, if you don't already, I was possibly looking to use the material, and was just looking for proper citation. I really do think the exercise is mentioned somewhere, although I can't find where, which leads to the question.

     – Paul Burchett Feb 07 '17 at 00:07
  • Two of the three votes are "unclear what you're asking". With the below answer, it should be clear with the diagrams what I'm asking for both questions. – Paul Burchett Feb 07 '17 at 00:27

1 Answers1

3

Not in 3D and not super-fancy, but it should get across the point. I did not do it for the rook because as you note the rook always has 14 squares to go to (on an empty board).

However if you want to use this to argue for putting pieces in the center, I'd be careful, because:

  • This is for an empty board. Lots of things can happen when other pieces are on the board.
  • The illustration for the king is probably of limited value because (unless you are Steinitz) we don't usually think of the king as an active piece.
  • For the queen and bishop (which are essentially the same, only shifted by 14, the number of rook moves) you notice that the difference between different squares (center and border) is not all that great. In my opinion a much more important factor for positioning queen and bishop centrally in a real game is that they have more options, i.e. a bishop in the center can go in four directions while a bishop in the corner has only one direction. This means that a bishop in the center can attack things in all four directions and likewise in order to block this bishop, the opponent has to block four directions. Also for transferring the bishop to other parts of a board a central position might be better.
  • For the knight there could be some value in this as it cannot be blocked by other pieces, so the situation for a knight is essentially the same as on an empty board. That's where you get the saying: "A Knight on the rim is dim" from. But as with all such rules there are plenty of exceptions.

King Knight Queen Bishop

user1583209
  • 20,735
  • 3
  • 41
  • 97
  • I've seen these in my work a lot. Do you happen to know who first considered the exercise? – Paul Burchett Feb 05 '17 at 19:06
  • @PaulBurchett: I have no idea who that would be. – user1583209 Feb 05 '17 at 21:14
  • I upvoted you for the diagrams. I should mention that I thought I saw this exercise mentioned somewhere. I should clarify, certainly one doesn't just take the center regardless of material. One positions, perhaps delays by blocking the center. However, those center four squares, if truly controlled, often lead one to victory. – Paul Burchett Feb 05 '17 at 22:07
  • One can also counterattack the center, as the hypermoderns. But much play ultimately revolves around the center, or at least taking it out of the opponents hand, unless tactics dictate otherwise. – Paul Burchett Feb 05 '17 at 22:20
  • @Paul Burchett I fully agree that the center is important; but not for the reason suggested by these diagrams (except perhaps in case of the knight). – user1583209 Feb 05 '17 at 22:26
  • These in part show it. Certainly the board can be closed with pawns, but it is a condition that's nearly reached often in a good endgame. Piece mobility is important and is partly illustrated in the diagrams. – Paul Burchett Feb 05 '17 at 22:35