Raoult’s Law ($p_A = \chi_A \cdot p_A^\circ$) becomes a special case of Henry’s Law ($p_A = K_H^{px} \cdot \chi_A $) when $K_H^{px} = p^\circ_A$, but where do these laws differ from each other?
There’s a statement in my text book which I’m having trouble understanding.
The statement:
As a real solution approaches the limit of infinite dilution its components behave more ideal. The solvent obeys Raoult's law whereas solute (minor component) obeys Henry's law for dilute solutions.
Raoult's law can be seen to be valid for ideal liquids. The assumption behind Raoult's law is that both the liquid phase and the vapour phase behave ideally. This means that the interaction between any two molecules in the liquid and the vapour have no interaction. The Raolt's law just states the mole fraction of a component in the liquid phase is proportional to the mole fraction of the same component in the vapour phase. This is valid only for mixtures of ideal liquids. When you add a very small amount of impurity in a solvent (equivalent to infinite dilution) the interaction between the impurity and the solvent molecule is minuscule or technically infinitesimal. Therefore, the liquid still behaves ideally. Hence Raoult's law is applicable for the solvent.
Whereas Henry's law is also defined for a ideal mixture only this time the assumption is that the mole fraction of the component is tending to zero. this means that when very few molecules a present in a vast space, the interaction between them is almost zero. This makes the system ideal. therefore, an infinitesimally small quantity of impurity does not feel any interaction with another molecule of the same impurity in the solvent. Therefore, Henry's law is used for the solute. That is why Henry's law constant have huge values. Huge values makes sure that even small amount of the solute is accounted for when calculating the mixture properties.
For further clarity, please refer to chapter 6 of 'Molecular Thermodynamics of Fluid phase equilibria' by John M.Prausnitz et. al.
Raoult's and Henry's laws are limiting laws, generally applicable when the solute concentration goes to zero. In this limit the vapor pressure of any component in the solution depends linearly on its mole fraction, implying the absence of solute-solute interactions.
Raoult's law describes the dependence of the vapour pressure of a solvent as a function of its mole fraction $\chi_1$:
$$\lim_{\chi_1\rightarrow1}\left( \frac{p}{\chi_1}\right) =p^\ast$$
where $p^\ast$ is the vapour pressure of the pure solvent.
Henry's law describes the dependence of the vapour pressure of a solute as a function of its concentration. In terms of mole fraction $\chi_2$:
$$\lim_{\chi_2\rightarrow0}\left( \frac{p}{\chi_2}\right) =K$$
For a binary mixture of pure substances it can be shown that the laws are complementary: if one law holds for one component then the other law holds for the other component. It can also be shown that the laws imply that the solution satisfies other criteria for ideality, including zero enthalpy and volume of mixing.
Compare and contrast
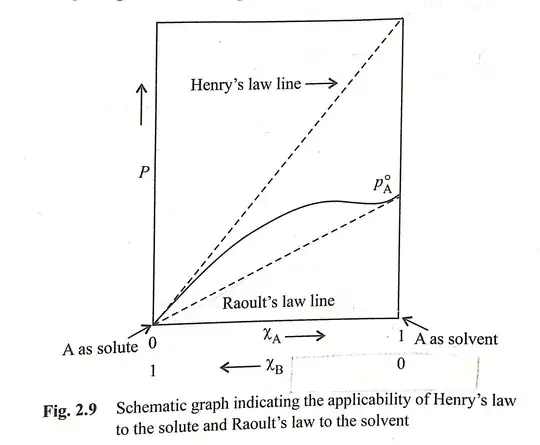
As stated in the caption of the figure posted by the OP, Henry's law applies to the solute and Raoult's law applies to the solvent. If a solute is non-volatile (e.g. sucrose or sodium chloride), Raoult's law still works, but invoking Henry's law, while possible technically (by setting Henry's constant to zero), would be kind of pointless.
As you can see for the example shown in the picture posted by the OP, Henry's law describes the partial pressure of a component at very low concentration. On the other hand, Raoult's law describes the pressure of a component at a concentration close to pure liquid.
Raoult's law is independent of the nature of the solute; the only parameter is the mole fraction of the solvent (or solute, if written as $\Delta p = \chi_\mathrm{solute} \cdot p^\circ$). Henry's law, on the other hand, depends on the nature of both solute and solvent (i.e. the Henry's constant is different for different solvents).
Continuous transition from Henry's to Raoult's law
For a binary system where both components are volatile, are liquid in the pure state and are miscible across the entire range, you can discuss the equivalence or non-equivalence of the two laws. The situation for the ethanol: water mixture is shown below:
The figure was taken from R K Thomas's course page, which has a great explanation of the entire topic. Note that the vapor pressure of either component increases linearly near 0% and 100% composition, but not with the same slope. In this particular case, both water and ethanol show positive deviation from Raoult's law at low concentration. There are also cases of negative deviation such as the chloroform: acetone system.
The case described by the OP, where components conform to Raoult's law for any composition, is realized for mixtures of the same molecule with different isotopic composition, e.g. ethanol with carbon-13 on the first or second carbon. To a good level of approximation, the boiling points of the two species are identical, and the interactions between identical or isotopically different molecules are the same, so Raoult's and Henry's law would give the same values. I don't know of a less trivial system (i.e. where the boiling points of the pure components differ) where that is the case.
[quoted in OP's question] As a real solution approaches the limit of infinite dilution its components behave more ideal. The solvent obeys Raoult's law whereas solute (minor component) obeys Henry's law for dilute solutions.
I don't think this statement is true. Henry's law does not require ideal behavior (the solute: solvent interaction can be stronger or weaker than the solvent: solvent interactions), and the distinct Henry's law constants depending on solvent reflect that. For example, more oxygen will dissolve in water than in cyclohexane at the same partial pressure of oxygen. The range where Henry's law applies is called ideally diluted solution. Roult's law will apply for any solute, so it also does not require an ideal solution.
If the solution is ideal (no difference between solvent: solute and solvent: solvent interactions), the condition $K_H^{px} = p^\circ_A$ mentioned in the OP's question becomes true.