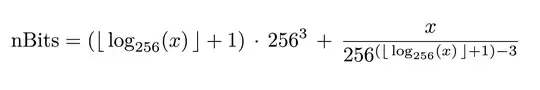3

I was wondering how the nBits are calculated from the target, I know how the the target is calculated from nBits, but how is the nBits calculated from the target?

Murch
  • 75,206
  • 34
  • 186
  • 622
CJ-Programmer
  • 71
  • 3
  • Does one of these answer your questions: https://bitcoin.stackexchange.com/a/57186/5406, https://bitcoin.stackexchange.com/q/8806/5406, https://bitcoin.stackexchange.com/a/61951/5406? – Murch Feb 19 '23 at 17:13
  • No, I was asking how the target is compressed into nbits, not the other way around. – CJ-Programmer Feb 20 '23 at 05:12

2 Answers2

3

You can calculate nBits from the target value by first taking its base 256 logarithm and rounding that to the next higher number, which will give you the first Byte out of four, the exponent, of nBits. You now know how many trailing Bytes you can cut off the target (the exponent minus three) and you're left with the mantissa.

Putting that into a closed formula is a bit messy in my opinion. The existing formula for calculating the target is not very nice in the first place, since it actually tries to express an algorithm. But here you go (x being the target):

nbits_formula

Example with the current nBits value 0x17073039:

x = 0x730390000000000000000000000000000000000000000

(floor(log(x, 256)) + 1) * 0x1000000 = 0x17000000


x / 256 ^ (0x17 - 3) = 0x73039


nBits = 0x17000000 + 0x73039 = 0x17073039

Please note that this formula does not work for all values. The mantissa, being a signed integer, should not exceed 2^23 - 1, which is why the exponent needs to be adjusted where this would be the case; e.g. for the maximum target 0x1d00ffff, where the expected exponent of 0x1c would lead to a mantissa of 0xffff00 and thus be interpreted negative.

sutterseba
  • 394
  • 1
  • 7
  • 2
    The top bit of the mantissa is a sign bit, so the exponent has to be such that the rounded mantissa value is between 2^15 and 2^23-1 (because values above 2^23 are treated as negative). That's why the genesis nBits has an exponent that's seemingly off by one. – Pieter Wuille Feb 20 '23 at 15:01
  • 1
    That makes sense, thanks! There probably isn't an obvious fix to the formula to catch this, is there? At least without complicating it too much. – sutterseba Feb 20 '23 at 15:20
  • Thank you for that. I've tried putting in some example targets and sometimes it has worked, sometimes it hasn't. – CJ-Programmer Feb 22 '23 at 12:14
  • You have to check the mantissa as Pieter described in his answer and adjust the exponent accordingly – sutterseba Feb 22 '23 at 21:00
1

I believe the algorithm is this:

  • Let b be the number of bits in the target: b = ⌈ log2(target+1)⌉.
  • Let e be the exponent: e = ⌊ (b/8)+1⌋.
  • Let m be the mantissa: m = ⌊ target/(256e-3)⌋
  • The nBits value encodes both m and e: nBits = 224e + m.

The computed mantissa should always be between 215 and 223-1. If it's larger, it would be interpreted as negative. If it's smaller, a lower exponent would provide more accuracy.

Pieter Wuille
  • 105,497
  • 9
  • 194
  • 308