Both the temperature and the density of a toy universe can, in a way, be linked to the age of the universe ($t$). Certain properties of the universe are dependent upon a scale factor $a(t)$ that is a function of time. The expansion of such a universe can be written in the Friedmann-Lemaitre-Robertson-Walker (FLRW) metric, generally written as
$$ds^2 = dt^2 - a(t)^2(d\Sigma^2)$$
where, in spherical coordinates, $d\Sigma$ is given by
$$d\Sigma^2 = \frac{dr^2}{1-kr^2} + r^2d\theta^2 + r^2\sin^2\theta d\phi^2$$
where $k$ is a constant. This shows that, in a toy universe, $r$ and $dr$ is proportional to $a(t)$, and so in a perfectly spherical toy universe, you could relate the volume to $t$. We know that, for a sphere,
$$V=\frac{4}{3}\pi r^3$$
and because $d\Sigma^2$ (and by extension $r^2$) is related to $a(t)^2$, we can relate volume to time. If you knew the mass-energy of the universe, you could then relate the change in density to $t$. Unfortunately, our universe does not appear to be perfectly spherical, and so this may not apply.
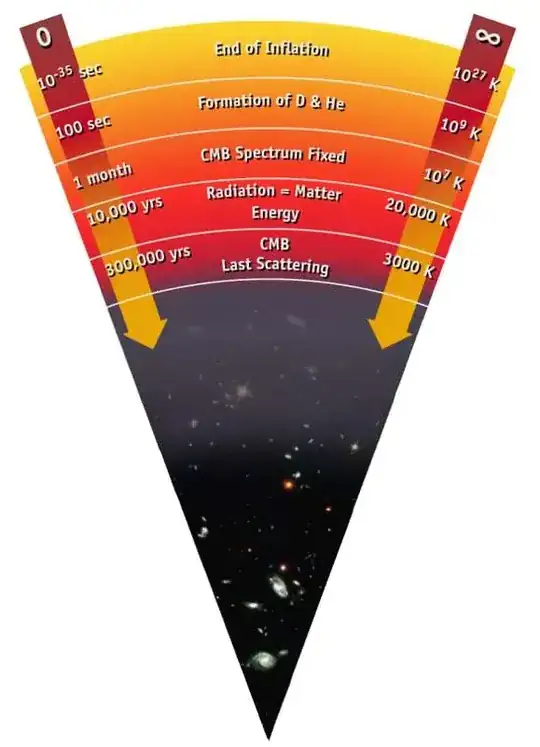
You can relate something else to the age of the universe: the temperature of the cosmic microwave background. It has cooled over time, and is presently at about 2.7 Kelvin. While the temperature of the CMB may not be governed by the scale factor $a(t)$, it is certainly governed by time, and thus one you could in fact write the temperature of the universe as function of time. Unfortunately, I haven't been able to find data on the evolution of the CMB, but I can try, and perhaps this will lead you to an answer.
To summarize: In a perfectly spherical universe, assuming you know the matter-energy content and the scale factor $a(t)$, you could write an equation for the density of the universe. In any universe, you can also write an equation for the temperature of the CMB - the "temperature of the universe".
I hope this helps.
Source for FLRW metric: http://www.universe-galaxies-stars.com/Robertson-Walker_coordinates.html
 .
.