1

I'd like to use Solidworks to create a cam (peanut looking) for computing the equation of time in a pocket watch. Would appreciate any point to the right direction or advice.

Audemars Piguet EoTInner workings of the same watch

Brendan Darrer
  • 227
  • 1
  • 8
noob_watchmaker
  • 21
  • 4
  • 4
    I'm not sure: what is the Astronomy part of the question? How does the Image illustrate your question or Problem? What did you try? – planetmaker Mar 28 '24 at 04:08
  • 2
    Not sure what your actual goal is here. The equation of time is used to correct a sundial to give clock time, but if you have a pocketwatch, you already know clock-time. – James K Mar 28 '24 at 06:49
  • 2
    @JamesK Presumably, the OP's goal is to make a watch that has a dial showing solar time (or just the EoT correction). FWIW, in the early days of mechanical clocks, the EoT was used to correct clock time to "proper" sundial time. – PM 2Ring Mar 28 '24 at 10:15
  • 2
    There are equations for computing the EoT, with various levels of accuracy. I have EoT code in Python (and much simpler code here), but I have no idea how to turn that into clockwork mechanism. – PM 2Ring Mar 28 '24 at 10:23
  • 2
    You might try reaching out to the author of this post if he doesn't see this: https://astronomy.stackexchange.com/questions/57180/how-can-i-build-a-gear-based-mechanism-to-calculate-solstices-equinoxes-and-cr – Greg Miller Mar 28 '24 at 13:00

1 Answers1

4

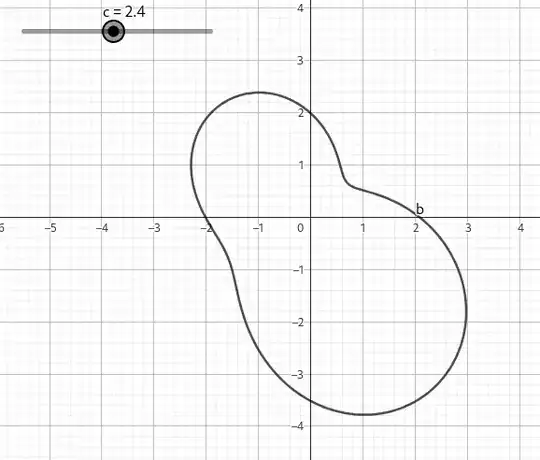
Following the video, the shape of the cam is a polar plot of the equation of time, with an offset to keep the values positive. You can use any of the trigonometric approximations to the equation of time to plot this, with your choice of offset (presumably a smaller offset makes more deeply indented cam that is hard to follow, but a larger offset makes a cog that is easy to follow, but heavier and takes up more space. So the exact shape is a practical and engineering decision.

You can plot the polar curve with your favourite graph plotter. Here is a quick mockup with geogebra and a simple formula adapted from wikipedia, $$r = c -0.7659\sin(6.24+0.0172 d)+0.9863\sin(2( 6.24+0.0172 d)+3.5932)$$

enter image description here

In which $c$ is the offset to keep the radius positive and $d$ is days of the (Julian) year $0\le d<365.35$.

How that shape is then used to adjust a clockwork mechanism is hinted at by the video, but well beyond my knowledge of clocks (and isn't an astronomical question)

James K
  • 120,702
  • 5
  • 298
  • 423
  • 1
    one thing I notice is that this is plotted anticlockwise (positive increasing angle) but the clock, or course, works clockwise, so their cam is like the mirror image of this. – James K Mar 28 '24 at 18:48
  • 1
    Hi James, thank you for taking the time to provide an answer to my post. I apologize for not having made it more specific. But I'm glad you immediately knew what information to provide. This is going to help a lot. Thanks again. If you or anyone else is interested to see what this is about, follow on Instagram @noob_watchmaker. – noob_watchmaker Mar 29 '24 at 20:54