The Ascendant-Descendant axis is the line of intersection of the ecliptic plane with the rational horizon. The ecliptic is the plane of the Earth's orbit. The rational horizon is the plane through the geocentre (the Earth's centre) which is parallel to the observer's local horizon. So the Ascendant-Descendant axis passes through the geocentre. The Ascendant is to the east, the Descendant is to the west. Hence the Ascendant is the point on the ecliptic that is currently rising.
Here's a diagram from an article on the Astrodienst site, Astronomical Foundations of the Astrological Houses, by Christopher A. Weidner.
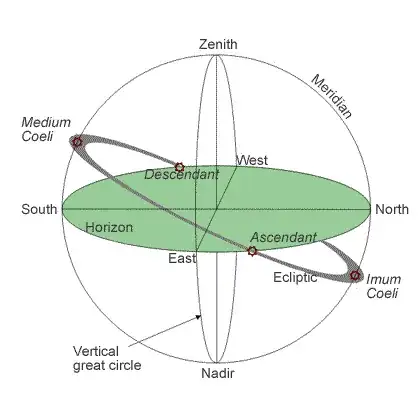
We can easily calculate the Ascendant using spherical trigonometry. Wikipedia gives the equation, but it's in a slightly misleading format. Here's a better version:
$$\lambda_{\rm Asc} = \arctan \left(\frac{\cos\theta_{\rm L}}{-(\sin\theta_{\rm L} \cos\varepsilon + \tan\phi \sin\varepsilon)} \right)$$
where $\theta_{\rm L}$ is the local sidereal time, expressed as an angle, $\varepsilon$ is the obliquity of the ecliptic, and $\phi$ is the latitude of the observer (north positive, south negative).
The mean rotation of the Earth relative to the stars is 360° in 24 sidereal hours. So we can convert sidereal time in hours to sidereal time in degrees by multiplying by 15.
The local sidereal time can be calculated by adding the observer's longitude to the Greenwich sidereal time (east longitude positive, west longitude negative). Of course, for this equation to make sense both quantities must be in the same units, so we need to divide the longitude in degrees by 15 to convert it to hours. Conversely, we can just multiply the sidereal time by 15 to convert it to degrees, since we need it in angle format for the Ascendant calculation.
So,
$$\theta_{\rm L} = \theta_{\rm G} + \lambda$$
where $\theta_{\rm G}$ is the Greenwich sidereal time expressed as an angle in degrees, and $\lambda$ is the longitude of the observer (in degrees).
We also need the obliquity of the ecliptic. Wikipedia gives various polynomial expressions. The equation from the Astronomical Almanac for 2010 is good for several centuries either side of the present era. There's also an equation from Laskar which is less precise, but it's valid for a span of 10,000 years.
The Greenwich Mean Sidereal Time (GMST) can be computed using a polynomial given in the JPL Horizons manual.
I need to digress briefly to discuss the ecliptic coordinate system. The ecliptic is the Earth's orbital plane, so the Sun's apparent path lies on the ecliptic. The Moon's orbit is inclined by ~5.145° to the ecliptic, so the Moon is always within 5.145° of the ecliptic, and all the planets are within 8° of the ecliptic, as I mention in this answer.
The band 8° either side of the ecliptic is known as the zodiac. In the ecliptic coordinate system the position of a point on the celestial sphere is given in terms of ecliptic longitude and ecliptic latitude. The ecliptic longitude is zero at the March equinox point, and increases in the direction of the Sun's motion. The ecliptic latitude gives the angular distance above or below the ecliptic (north positive, south negative).
Modern astronomy prefers to locate points on the celestial sphere using the equatorial coordinate system of Right Ascension (RA) and Declination, which is based on the celestial equator plane rather than the ecliptic. The March equinox point has zero RA and zero declination. Declination gives the angular distance above or below the celestial equator. This system became prominent after the invention of the telescope. It's very convenient when using a telescope with an equatorial mount.
However, for most of history, the ecliptic coordinate system was the main way to specify celestial points. It goes back to the ancient Babylonian astronomers, if not earlier.
You can give ecliptic longitude in degrees, but it was traditional to use zodiac notation. This notation has fallen out of use in astronomy, but it's still very popular in astrology. This notation simplifies the arithmetic of calculating the angle between two longitudes.
In zodiac notation, the ecliptic is divided into 12 equal sections of 30°. These sections are called signs, and they're named after the constellations near the zodiac. In ancient times, the signs roughly corresponded with the constellations, but they've drifted out of sync in the last couple of millennia, due to the precession of the equinoxes.
The first sign is Aries, the second sign is Taurus, etc. In zodiac notation, ecliptic longitude of 10°20' is written 10 Aries 20. Ecliptic longitude 45°10` is written 15 Taurus 10. Etc. It's traditional to write zodiac notation using the traditional sign symbols. (There are Unicode glyphs for these symbols, but they're a bit bulky, in my opinion).
The March equinox point is 0 Aries 0. It's often called the First Point of Aries, even in modern astronomy. Why the first point? This system is ancient! It was devised long before zero was invented. :)
The sign containing the Ascendant is known as the rising sign. It's literally the section of the ecliptic which is currently rising on the rational horizon.
Here's a Python script which calculates the obliquity, GMST, local sidereal time, and the ascendant. You must supply the time in UTC, not local time. The script uses Sage features to read the date & time and location data from the GUI, but the rest of the program is plain Python. It uses the standard datetime module to parse the date & time, but it uses no 3rd party libraries.
The date must be given in YYYY-Mon-DD format. That is, a 4 digit year, followed by the 3 letter abbreviation of the month name, followed by a 1 or 2 digit day, with - between the fields. The UTC time field is a little more flexible. It may be specified with or without seconds, and you may specify fractional seconds, with upto 6 digits after the decimal point.
Latitude and longitude must be given in decimal degrees. However, you can write arithmetic expressions in those input boxes. For example, you can input 40°N 43' latitude as 40 + 43/60.
The script prints the Ascendant in both zodiac notation and degrees.
""" Calculate the ascendant from the UTC time and location
The ascendant is the ecliptic longitude on the rational horizon
See https://en.wikipedia.org/wiki/Ascendant
Obliquity & sidereal time equations from JPL
Written by PM 2Ring 2024.02.01
"""
from datetime import datetime, timedelta, timezone
from math import sin, cos, tan, atan2, degrees, radians
def parse_datetime(dtstr):
for tfmt in (' %H:%M', ' %H:%M:%S', ' %H:%M:%S.%f', ''):
try:
dt = datetime.strptime(dtstr, '%Y-%b-%d' + tfmt)
break
except ValueError:
continue
else:
print("Bad date time string:", dtstr)
return None
return dt.replace(tzinfo=timezone.utc)
def hms(t):
h = int(t)
t = 60 * (t - h)
m = int(t)
t = 60 * (t - m)
return f"{h:>2}:{m:02}:{t:06.3f}"
zodiac = "Ari Tau Gem Can Leo Vir Lib Sco Sag Cap Aqu Pis".split()
def sdms(t):
z = int(float(t) // 30)
t -= 30 * z
d = int(t)
m = 60 * (t - d)
return f"{d:2} {zodiac[z]} {m:4.1f}"
J2000 epoch
day_zero = datetime(2000, 1, 1, 12, tzinfo=timezone.utc)
@interact
def _(txt=HtmlBox('<h3>Ascendant</h3>Date format: YYYY-Mon-DD'),
dtstr=('Date & Time, UTC', '2000-Jan-1 12:00'),
lat=('Latitude', 51.4773207),
lon=('Longitude (east)', 0.0),
auto_update=False):
dt = parse_datetime(dtstr.strip())
if dt is None:
return
lon, lat = float(lon), float(lat)
# Convert to days since Noon, 1 Jan 2000
d = (dt - day_zero).total_seconds() / 86400
# Julian centuries
T = d / 36525
# Obliquity of the ecliptic. T should be Terrestrial Time
oe = ((((-4.34e-8*T - 5.76e-7)*T + 0.0020034)*T - 1.831e-4)*T - 46.836769)*T / 3600 + 23.4392794444444
oer = radians(oe)
print("Obliquity:", oe)
# Greenwich Mean Sidereal Time
gmst = (67310.548 + (3155760000 + 8640184.812866) * T
+ 0.093104 * T**2 - 6.2e-6 * T**3) / 3600 % 24
print('Greenwich sidereal time:', hms(gmst))
lst = (gmst + lon / 15) % 24
print(' Local sidereal time:', hms(lst))
# Local sidereal time, in radians
lstr = radians(lst * 15)
# Ascendant
ascr = atan2(cos(lstr), -(sin(lstr) * cos(oer) + tan(radians(lat)) * sin(oer)))
asc = degrees(ascr) % 360
print(f"Ascendant: {sdms(asc)} = {asc}°")
I've tested this script against various online calculators, including the Sidereal Time service of the USNO. My sidereal times agree with the USNO values to sub-second precision.
Here's a live version of the script, running on the SageMathCell server.
