At the equator, there is no geometric effect at all—the Sun's daily track above the horizon is always exactly half a circle.
The issue is the definition of "half a circle". What this refers to is how long the Sun (or any star for that matter) is above the horizon when the observer is at the equator. If you ignore atmospheric refraction and use the center of the Sun, then sunrise to sunset (or star rise to star set) is 12 hours long. 12 hours is half of 24 hours, so that is half a circle.
Let's take an extreme example. Polaris is approximately 0.7 degrees from the celestial north pole. Therefore, Polaris travels in a small circle (radius of 0.7 degrees) around the pole. It does not move very much. But Polaris is visible for 12 hours from rising to setting, so it is visible for exactly half a circle.
Another way to express this is by using the hour angle when the object rises or sets. The hour angle is the number of degrees (or hours of right ascension) between the object and the meridian. Specifically, the angle is measured between two planes:
- The plane of the meridian. The meridian is the lighter red line in the figures below, connecting due north (N), the zenith (Z), and due south (S).
- The plane passing through celestial north, the object in question, and celestial south.
When the observer is at the equator, all objects have an hour angle of 6 hours when rising.
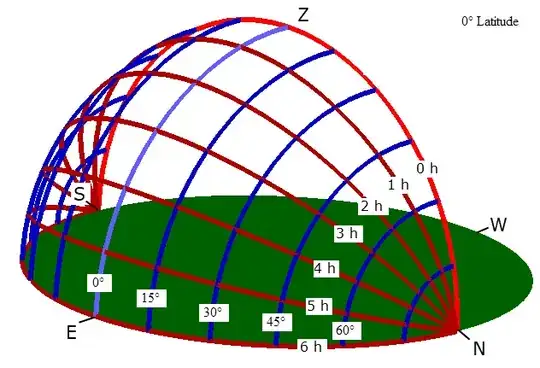 Figure 1: Observer at the equator. If the line of 0h Right Ascension (RA) is on the meridian (the lighter red line), then 6h RA is on the horizon all the way from due north (N) to east (E) to south (S). Any object that is rising has an hour angle of 6h. (This is true regardless of what line of RA is on the meridian.) Likewise, the hour angle is 6h when setting. 6h+6h=12h which is half of a full circle of 24h.
Figure 1: Observer at the equator. If the line of 0h Right Ascension (RA) is on the meridian (the lighter red line), then 6h RA is on the horizon all the way from due north (N) to east (E) to south (S). Any object that is rising has an hour angle of 6h. (This is true regardless of what line of RA is on the meridian.) Likewise, the hour angle is 6h when setting. 6h+6h=12h which is half of a full circle of 24h.
For observers north of the equator,
- Objects north of the equator have an hour angle larger than 6 hours when rising. Therefore, they are visible for more than "half a circle".
- Objects south of the equator have an hour angle smaller than 6 hours when rising. Therefore, they are visible for less than "half a circle".
 Figure 2: Observer at +30 degrees latitude. The blue lines are declination lines; the lighter blue line at 0 declination is the celestial equator. The hour angle of an object that is rising depends on the declination of the object. When the Sun is at +23 degrees declination, the hour angle is approximately 7h. When the Sun is at -23 degrees declination, the hour angle is approximately 5h. When the Sun is at 0 degrees declination, the hour angle is 6 hours, and this is true regardless of the observer's latitude (except at the poles).
Figure 2: Observer at +30 degrees latitude. The blue lines are declination lines; the lighter blue line at 0 declination is the celestial equator. The hour angle of an object that is rising depends on the declination of the object. When the Sun is at +23 degrees declination, the hour angle is approximately 7h. When the Sun is at -23 degrees declination, the hour angle is approximately 5h. When the Sun is at 0 degrees declination, the hour angle is 6 hours, and this is true regardless of the observer's latitude (except at the poles).
Time from rising to the meridian. There is a relationship between the hour angle and the time between when an object rises and when it reaches the meridian.
- For stars and planets (which move slowly day to day), consider these objects as being attached to the dome of the sky. Since the sky rotates through 24h RA in 23 hours 56 minutes of clock time, the clock time approximately equals the hour angle. (That is, 24h RA/23.93h clock time approximately equals 1.)
- By definition of "noon", the Sun appears to move 360 degrees (or 24h RA) around the sky in 24 hours of clock time. Thus, the time from rising to reaching the meridian equals the hour angle. At 0 latitude, Figure 1 shows that the Sun always rises 6 hours prior to noon, regardless of the date. At other latitudes, the time depends on the declination of the Sun, but the time always equals the hour angle.
- For the Moon, the hour angle when rising is still shown by Figure 1 (always 6h) and Figure 2 (depends on the declination). But the Moon requires approximately 25 hour to rotate through 360 degrees (24h RA). Therefore, the time between moonrise and reaching the meridian is approximately 25/24=1.04 times longer than the hour angle.
As mentioned at the beginning, sunrise (and moonrise) is based on when the limb of the Sun (or Moon) becomes visible and includes the effect of atmospheric refraction which makes the object appear to be higher in the sky. Also, observing from a high altitude where the horizon is more than 90 degrees from the zenith would affect the hour angle. All those types of effects are ignored in the previous discussion.

