I think the argument with Rayleigh scattering which scales with $\frac{1}{\lambda^4}$ and therefore producing more scattering of shorter wavelengths doesn't hold here because Rayleigh scattering is an approximation for particles (much) smaller than the wavelength. So it describes scattering on molecules, which for example explains the blue color of the sky in the absence of clouds.
Clouds consist of much larger particles, which are made up of a solid core called cloud condensation nucleus, which is surrounded by a water sphere. Usually we simply think of small water droplets. No idea what a typical diameter of water droplets in clouds is, I guess it's a distribution of all diameters between zero until the droplets become macroscopic and result in rain. Read somewhere that typical fog particles are in the range of several microns... Anyways, scattering on particles comparable or larger than the wavelength is described by Mie scattering, which has much less dependence on the wavelength than $\lambda^{-4}$ and therefore clouds are white (all wavelengths in the visible are scattered more or less to the same amount).
The math of Mie scattering is complicated, but fortunately there is a python module called miepython. It needs the complex refractive index of water, which can be found for example here. I downloaded miepython and did some calculations of light at 350 nm (UVA), 550 nm (Visible) and 10 $\mu$m, which is already long wave infrared (LWIR) and in the range thermal cameras work. Different droplet diameters are on the x-axis ranging from 0 to 0.1 mm (which is starting to get macroscopic). The result is this:
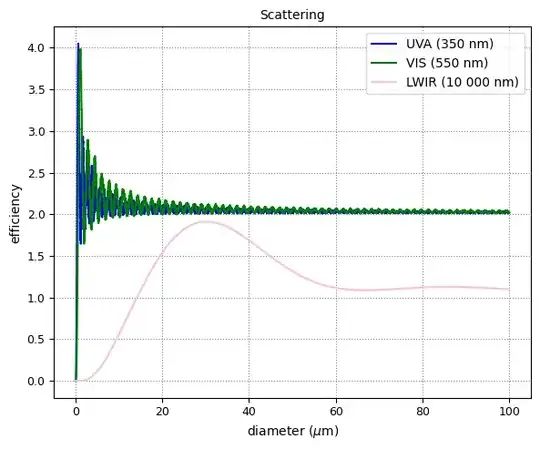
On the y-axis is the scattering efficiency per particle. To get a cross section you need to multiply by the geometric particle cross-section. To get then an extinction in unit 1/m you additionally need to multiply by the particle concentration (guess it's a distribution with much more small than large particles). But anyways, for a qualitative comparison this is enough. First thing to observe is that there are many oscillations, which is typical for Mie theory (as it assumes all particles to be round spheres with reflection and interference everywhere...). Apart from that, UVA and Vis are almost the same. However, when zoomed in

the Visible line seems to be on average a tiny bit larger than the UVA line. Which means an image would be a bit sharper in the UV, but this difference would be hardly visible in any real world image.
The real difference, as stated in the answer from uhoh before, comes with LWIR, which shows much less scattering, escpecially when particles are small (and I still think the majority of particles will be small). So this is somehow a proof of what was answered before by uhoh. UV won't work, but maybe give it a try with LWIR... (but as mentioned before the sun is not as bright in LWIR as it is in the Vis. Room-temperature emits at LWIR, so there might be a lot of different drawbacks as well).