Proportion of Lunar Fraction in a Year

Question

I grabbed a year of lunar fraction data from the USNO and binned the counts to find the shape of the curve as below

My understanding of lunar fraction was that 0.5 does not distinguish between the direction as it is a cycle from 0 (new moon) to 1 (full moon) then back to 0 (new moon). And therefore I assumed that 0.5 would have more counts than 0 or 1 like this

I trust the data and counts plot to be true but I cannot see what I am misunderstanding that would lead to this shape. Can anyone more knowledgeable than myself see my misunderstanding and/or explain the lunar fraction to me better?

Answer 1

Think how the terminator (the line between the light and dark) moves on the moon.

Thinking of the moon as a 3d ball, you know that the terminator must move around the moon at a constant rate. But we see a projection of the moon; we see the moon as a disc. So the terminator doesn't seem to move constantly. It appears to move most quickly at half moon and slowest at new moon and at full moon.

At full moon, the terminator is right at the extreme edge of the lunar disc, so it seems to move very slowly. At half moon, it is in the middle of the disc, and so seems to move quickly.

See how the meridians are closer together near the edge of the moon.

As the terminator seems to move quickly at half-moon, the lunar fraction is between 0.45 and 0.55 for less time than it is between 0.9 and 1 (for example)

In your diagram imagine tracing the curve, but moving most quickly through the middle, but slowly when turning the curve. You'll spend more time in the red, and least time in the green, resulting in the graph you get.

Answer 2

The illumination fraction is very close to a sinusoidal function of time. Plot the illumination fraction as a function of time such as illumination fraction versus day number of the year and you will see something very, very close to a sinusoid.

If it was exactly sinusoidal, the moon would spend about 29.5% of the time with more than 80% illuminated, another 29.5% of the time with less than 20% illuminated, but only 14.8% of the time with illumination between 40% and 60%. Note that all three of these are 20% illumination bins. The reason for this is that 50% illumination is exactly when the illumination fraction changes fastest.

My understanding of lunar fraction was that 0.5 does not distinguish between the direction as it is a cycle from 0 (new moon) to 1 (full moon) then back to 0 (new moon).

Another way to think about it that the time between 0% and 20% illumination also involves two key intervals: Going from 20% to 0%, and then from 0% to 20%, both of which are long intervals due to the sinusoidal nature of the illumination fraction curve. The intervals between 60% to 40% illumination and from 40% to 60% illumination are fast, again due to the sinusoidal nature of the curved.

Answer 3

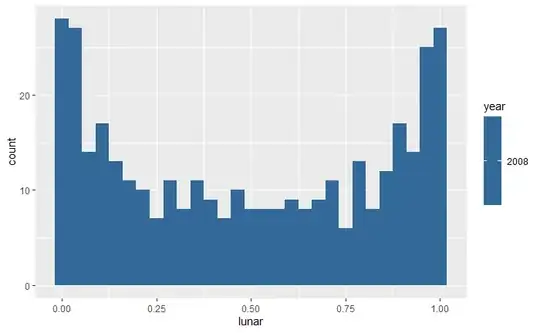
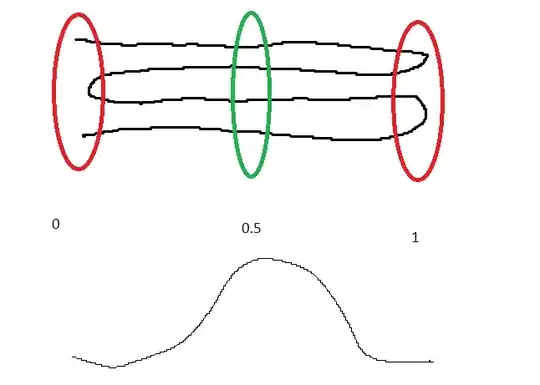
To put some math to it, as other answers note, the cycle is nearly sinusoidal (I guess factors like eccentricity of orbit and the oblate shape adjust it just a bit)

So we can use cosine or sine as the basic shape. So base it on $$f = \sin t$$ (with basically t being how far into the lunar month we are, and f being the result of how full the moon is)...

_{^{(More precisely, it'd be $f = \frac{\sin {\frac{2\pi}{S}t}+ 1}{2}$ to normalize the results to be between 0 and 1, and to convert from days to radians, but those factors don't alter the basic math ideas ahead, so will just stick with the basic trig function)}}

But instead of knowing the date and wanting to know how full the moon is, we are working from how full the moon is, and asking how many days it is there... so it's the inverse function we'd use:

$$t = \arcsin f$$

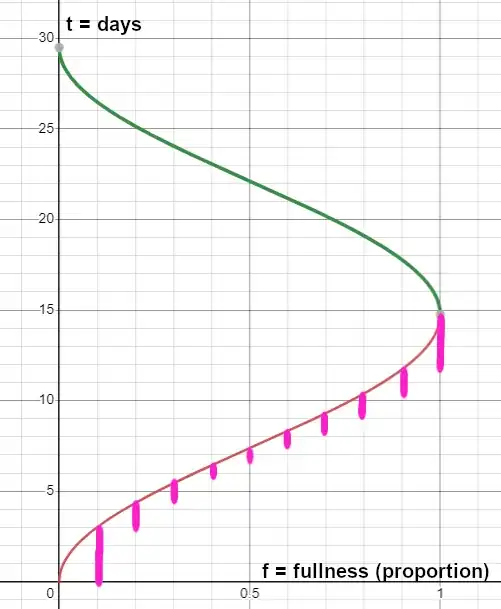
The pink is the amount of time in each bin. Note that the top half of the graph (itself needed added construction to arcsin, since otherwise it's not technically a function) isn't needed, as it has the same amounts as the bottom half.
The idea in the question that it spends more time in "green" zone than the "red" because it duplicates doesn't work... every spot on the graph is found 2 times in a cycle, except the singular points of absolute fullness and newness... and these are bins, not instantaneous points, so those two points mean infinitesimally nothing -- in other words if you extend your cycle worms a bunch more times, you'd see there's basically the same number of crossing through each green circle as the red, not double\more.

How do we calculate how much time it spends in bins? We want $\Delta t $ $(\equiv t_{f2} - t_{f1})$.
But what's nice is that $\Delta t$ is related to the chosen $\Delta f$ in slope... which calculus shows at any point is the derivative. So $\Delta t ≈ \Delta f \cdot dt/df$

What's the derivative of arcsin? $$\frac{dt}{df} = \frac{1}{\sqrt{1-f^2}}$$

And that has a graph shape of:

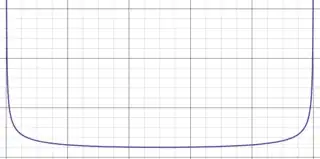
And viola, that's your shape.
Note that the derivative actually goes to infinity at the edges, the full and new moon... indicating that as you choose smaller and smaller bin sizes... the frequency graph would likewise be proportionally more and more dominated by those edges (infinitely so, if you chose infinitely small bins). For reasonable sized bins you just see a graph like yours!

So long story short, as others noted, sinusoidal functions change faster through the middle of the graph than the edges. That's why, for example, in midlatitude sites you'll actually see more days with extreme sunrise/sunsets than the middle ground 6 AM - 6 PM (solar noon) 12-hour period. Because again, the sunrise/sunset are changing much more quickly during the spring/autumn, meaning much fewer days in those middle values, than at the edges.